Common and Natural Logarithm

The common logarithm is a logarithm with base 10. It is denoted as log₁₀(x) or simply log(x). It is used to solve problems involving powers of 10.

The natural logarithm is a logarithm with base e, where e is the mathematical constant approximately equal to 2.71828. It is denoted as ln(x).

The relationship between logarithms and exponents is fundamental in mathematics. Logarithms and exponents are inverse operations, meaning they “undo” each other.

The following diagrams gives the definition of Logarithm: Common Log, and Natural Log. It also shows the relationship between logs and exponents. Scroll down the page for more examples and solutions.

Logarithms and exponents are inverse functions. This means:
If y = b^x, then x = log_b(y).
Similarly:
If x = log_b(y), then y = b^x.

Common Logarithms

Logarithms to base 10 are called common logarithms. We often write “log₁₀” as “log” or “lg”. Common logarithms can be evaluated using a scientific calculator.

Recall that by the definition of logarithm.
log Y = X ↔ Y = 10^X

Natural Logarithms

Besides base 10, another important base is e. Log to base e are called natural logarithms. “log_e” are often abbreviated as “ln”. Natural logarithms can also be evaluated using a scientific calculator.

By definition
ln Y = X ↔ Y = e^X

Using a calculator, we can use common and natural logarithms to solve equations of the form a^x = b, especially when b cannot be expressed as aⁿ.

Example:
Solve the equations
a) 6^{x + 2} = 21
b) e^2x = 9

Solution:
a) 6^{x + 2} = 21
log 6^{x + 2} = log 21
(x + 2) log 6 = log 21

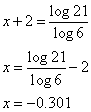
b) e^3x = 9
ln e^3x = ln 9
3x ln e = ln 9
3x = ln 9

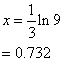
Example:
Express 3^x(2^2x) = 7(5^x) in the form a^x = b. Hence, find x.

Solution:
Since 3^x(2^2x) = 3^x(2²)^x = (3 × 4)^x = 12^x the equation becomes

12^x = 7(5^x)

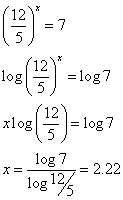
Common And Natural Logarithms

We can use many bases for a logarithm, but the bases most typically used are the bases of the common logarithm and the natural logarithm. The common logarithm has base 10, and is represented on the calculator as log(x). The natural logarithm has base e, a famous irrational number, and is represented on the calculator by ln(x). The natural and common logarithm can be found throughout Algebra and Calculus.

Defines common log, log x, and natural log, ln x, and works through examples and problems using a calculator.

• Show Video Lesson

Common And Natural Logarithms

Example: Write the following logarithms in exponential form. Evaluate if possible.

Properties Of Logarithms

The logarithm of a Product:
log_bMN = log_bM + log_bN

The logarithm of a Quotient:
log_bM/N = log_bM - log_bN

The logarithm of a number raised to a power:
log_bM^P = P log_bM

How to use the properties of logarithms to condense and solve logarithms?
How to use the properties of logarithms to expand logarithms?

• Show Video Lesson

Common And Natural Logs

Examples:
Solve without a calculator:
log₃3
log 1
log₁₆2
ln e³

Solve with a calculator:
log 3
log 32
ln √5
ln 7.3

• Show Video Lesson

How to solve logarithmic equations?

The first example is with common logs and the second example is natural logs. It is good to remember the properties of logarithms also can be applied to natural logs.

Examples:
Solve, round to four decimal places.

1. log x = log2x² - 2
2. ln x + ln (x + 1) = 5

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.