Logarithm Rules
In these lessons, we will look at four basic rule of logarithms (or properties of logarithms) and how to apply them. You may want to also look at the proofs for these properties.
Related Pages
Common And Natural Logarithm
Logarithmic Functions
Rules Of Exponents
Logarithm Properties
The following table gives a summary of the logarithm rules. Scroll down the page for more explanations and examples on how to use the rules to simplify and expand logarithmic expressions.
The rules of logarithms are:
1) Product Rule
The logarithm of a product is the sum of the logarithms of the factors.
loga xy = loga x + loga y
2) Quotient Rule
The logarithm of a quotient is the logarithm of the numerator minus the logarithm of the denominator.
loga 
= loga x – loga y
3) Power Rule
loga xn = nloga x
4) Change Of Base Rule
where x and y are positive, and a > 0, a ≠ 1
Example:
Simplify the following, expressing each as a single logarithm:
a) log 2 4 + log 2 5
b) log a 28 – log a 4
c) 2 log a 5 – 3 log a 2
Solution:
a) log 2 4 + log 2 5 = log 2 (4 × 5) = log 2 20
b) log a 28 – log a 4 = log a (28 ÷ 4) = log a 7
c) 2 log a 5 – 3 log a 2 = log a 52 – log a 23 = log a
Example:
Evaluate 2 log3 5 + log3 40 – 3 log3 10
Solution:
2 log3 5 + log3 40 – 3 log3 10
= log3 52 + log3 40 – log3 103
= log3 25 + log3 40 – log3 1000
= log3 
= log3 1
= 0
Example:
Given that log2 3 = 1.585 and log2 5 = 2.322, evaluate log4 15
Solution:
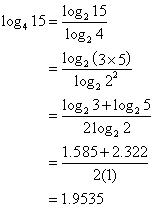
The Properties Of Logarithms And Applications
- loga 1 = 0 since a0 = 1
- loga a = 1 since a1 = a
- loga ax = x since ax = ax
The video explains explains and applies various properties of logarithms. The main focus is how to apply the product, quotient, and power property of logarithms.
Product property: The log of a product equals the sum of the logs.
Quotient Property: The log of a quotient equals the difference of the logs.
Power Property: The log of a power equals the product of the power and the log.
Examples on how to expand logarithmic expression and how to write expressions as a single logarithm.
- Expand the logarithmic expression.
log3(xy3/√z) - Write as a single logarithm.
2 lnx + 1/3 ln(x + 3) - 4 ln(2x)
Basic Logarithm Properties With Examples
Examples:
Expand the logarithmic expression.
log3(x/5) =
log7(2x) =
log5(x)4 =
log3(x/(yz)) =
log4(5√x) =
log3(xy)1/2 =
log2((x+1)/(y√z)) =
How to take an expression involving multiple logarithms and write it as an expression containing only a single logarithm?
Example:
Rewrite as a single logarithm
5 lnx + 13 ln (x3 + 5) - 1/2 ln(x + 1)
Introduction To The First Two Logarithm Properties: Product Law & Quotient Law
Property Three And Four Of Logarithms: Power Law & Change Of Base Law
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.