Logarithmic Functions

Related Pages
Common And Natural Logarithm
Properties Or Rules Of Logarithms
Rules Of Exponents
Logarithm Rules

What Are Logarithmic Functions?

We can think of logarithmic functions as the inverse of exponential functions.

The following diagram shows how logarithm and exponents are related. Scroll down the page for examples and solutions.

• Show Video Lesson On Introduction to Logarithmic Functions

How To Solve For X In Logarithmic Equations?

Equations of the form x = log_a y can be solved (for any of the three variables y, a or x) by first writing them in exponent form. We must be careful to check the answer(s) to see whether the logarithm is defined.

Take note of the following:

• Logarithms of a number to the base of the same number is 1, i.e. log_a a = 1
• Logarithms of 1 to any base is 0, i.e. log_a 1 = 0
• Log_a 0 is undefined
• Logarithms of negative numbers are undefined.
• The base of logarithms cannot be negative or 1.

Example:
Calculate the value of each of the following:
a) 1og₂ 64
b) log₉ 3
c) log₄ 1
d) log₆ 6
e) log₈ 0.25
f) log₃–9

Solution:
a) Let x = log₂ 64
2^x = 64
x = 6

b) Let x = log₉ 3
9^x = 3
x =

c) Let x = log₄ 1
4^x = 1
x = 0

d) Let x = log₆ 6
6^x = 6
x = 1

e) Let x = log₈ 0.25
8^x = 0.25

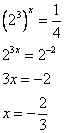
f) Let x = log₃– 9
3^x = – 9

Since it is not possible for 3^x to be negative, log ₃–9 is undefined.

Example:
Solve log_x 4 = 2

Solution:
log_x 4 = 2
x² = 4
x = 2 or –2

Since x is the base, x > 0 and x ≠ 1; so x = –2 is rejected and the only solution is x = 2

Example:
Solve log ₃ x = 2

Solution:
log ₃ x = 2
3² = x
x = 9

Example:
Solve log _x (4x – 3) = 2

Solution:
log _x (4x – 3) = 2
x² = 4x – 3
x² – 4x + 3 = 0
(x -1)(x – 3) = 0
So, x = 1 or 3

For the logarithm to be defined, the only solution is 3.

How to solve a logarithmic equation using properties of logarithms?
Just as we can use logarithms to access exponents in exponential equations, we can use exponentiation to access the insides of a logarithm. Solving logarithmic equations often involves exponentiating logarithms in order to get rid of the log and access its insides. Sometimes we can use the product rule, the quotient rule, or the power rule of logarithms to help us with solving logarithmic equations.

This video shows how solve a logarithmic equation using properties of logarithms and some other algebra techniques.

Example:
Solve 2log₃x - log₃(x + 6) = 1

• Show Video Lesson

How to solve a Logarithmic Equation with Multiple Logs?

When given a problem on solving a logarithmic equation with multiple logs, students should understand how to condense logarithms. By condensing the logarithms, we can create an equation with only one log, and can use methods of exponentiation for solving a logarithmic equation with multiple logs. This requires knowledge of the product, quotient and power rules of logarithms.

Example:
Solve log₇(x + 4) - log₇(x - 4) = log₇(5)

• Show Video Lesson

Techniques For Solving Logarithmic Equations

Examples:
a) log₃(x + 1) = 2
b) log₅(3x - 8) = 2
c) log(x + 2) + log(x -1) = 1
d) log x⁴ - log 3 = log(3x²)

• Show Video Lesson

More examples on solving logarithmic equations

Examples:
log₂x + log₂(x - 3) = 2
log(5x - 1) = 2 + log(x - 2)
ln x = 1/2 ln(2x + 5/2) + 1/2 ln 2

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.