Rules of Exponents or Laws of Exponents
In these lessons, we will learn five rules of exponent and how to use them to simplify expressions.
Related Pages
Exponents
Exponent Rules
Logarithmic Functions
More Math Lessons
Multiplication or Product Rule:
To multiply powers with the same base, keep the base the same and add the exponents.
Division or Quotient Rule:
To divide powers with the same base, keep the base the same and subtract the exponents.
Power of a Power Rule:
When a power has an exponent, keep the base the same and multiply the exponents.
Some of the Rules of Exponents or Laws of Exponents are summarized in the following table. Scroll down the page for examples and solutions on how to use the Rules of Exponents.

We will now consider combined operations of multiplication and division on numbers in exponent form, using all the rules of exponents introduced above.
Example:
Simplify the following expressions, giving your answers in exponent form:
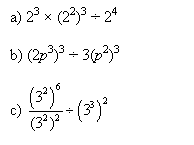
Solution:
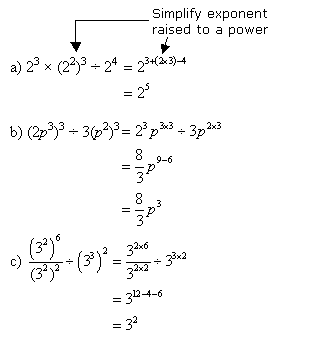
| Free Exponent Games Online | ||
|---|---|---|
| Multiply Exponents | Divide Exponents | Power of a Power |
| Power of a Product | Negative Exponents | Fractional Exponents |
How to simplify expressions using the Product Rule of Exponents?
The product rule of exponents states that to multiply exponential terms with the same base, add the exponents.
Example:
Write each of the following products using a single base. Do not simplify further.
- x2 • x4
- (-2)4 • (-2)1
- y4 • y5 • y
How to simplify expressions using the Quotient Rule of Exponents?
The quotient rule of exponents states that to divide exponential terms with the same base, subtract the exponents.
Example:
Write each of the following products using a single base. Do not simplify further.
- t7 / t3
- (-2)15 / (-2)12
How to simplify expressions using the Power Rule of Exponents?
Example:
Write each of the following products using a single base. Do not simplify further.
- (x3)2
- ((2y)4)3
- ((-3)4)6
How to simplify expressions using the Power of a Product Rule of Exponents?
Example:
Simplify each expression.
- (x3)2
- (3az)6
- (-4b5)2
- 1/(-2p)4
- (a-3b2)4
Example:
Simplify the following expressions:
a) (x2/2)4
b) (4n6)2
How to simplify expressions using the Power of a Quotient Rule of Exponents?
Example:
Simplify each expression.
- (2/x4)3
- (p3/q)4
- (-1/y3)12
- (m2n-4)3
- (3-2z-3)2
How to simplify expressions using the Quotient and Zero Exponent Rules?
Example:
Simplify each expression using the zero exponent rule. Assume all variables are nonzero.
How to simplify expressions using the Quotient and Negative Exponent Rules?
Example:
Write each quotient using a single base. Do not simplify further. Write all answers with positive exponents.
How to simplify expressions using the Product, Quotient and Zero Exponent Rules?
Example:
Write each expression using a single base. Do not simplify further. Write all answers with positive exponents.
Tutorial on the Basic Exponent Rules
Multiplication, Division, Power of a Power
Learn exponent rules through music and songs
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.