Area of Trapezoids
In these lessons we will learn
- how to find the area of trapezoids
- how to derive the area formula of a trapezoid
- how to solve problems using area of trapezoids
Related Pages
Area Of Polygons
Area Of Circles
Area Formulas
More Geometry Lessons
Geometry Worksheets
What is a trapezoid?
A trapezoid is a 4-sided polygon with two parallel sides. A trapezoid is also called a
trapezium (UK English).
How to find the Area of a Trapezoid?
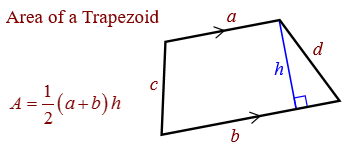
Given that side a is parallel to side b and h is the vertical height between a and b, the area of the trapezoid is given by the formula:
Example:
Find the area of the following trapezoid:
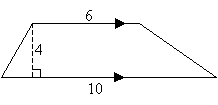
Solution:
Area of trapezoid
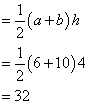
How to find the height of a trapezoid given the area?
Example:
Given that the area of the following trapezoid is 36. Find the value of h.
Solution:
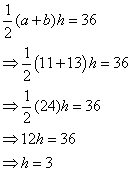
Worksheet to calculate the area of trapezoids.
Worksheet to solve trapezoid problems involving base1, base2, height and area.
How to find the area of a trapezoid using the formula 1/2(a + b)h?
Step 1: Find the bases and height. (The height must be perpendicular to bases)
Step 2: Add the bases and multiply by the height.
Step 3: Divide the answer by 2.
Step 4: Write the units.
Find the area of trapezoid
Find the height of a trapezoid given its area
Find the height of the trapezoid shown below, if the area is 378.56
Derive the area formula of a trapezoid
How to derive the area formula of trapezoid by using the area of triangles?
How to derive the area formula for a trapezoid using either two triangles or a parallelogram?
Problems involving area of trapezoid
The following video shows a problem involving the area of a trapezoid.
Example:
The area of a trapezoid is 91 and the height is 14.One of the bases has a length of 10.
Find the length of the other base.
Example:
The area of a trapezoid is 220 sq. ft. The length of the bases are 10 and 45 ft. Find the
height/altitude of the trapezoid.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.