Algebra: Work Word Problems

Work Problems are word problems that involve different people doing work together but at different rates. If the people were working at the same rate then we would use the Inversely Proportional Method instead.

The formula for “Work” Problems that involve two persons is

This formula can be extended for more than two persons. It can also be used in problems that involve pipes filling up a tank.

"Work" Problems: Two Persons

Example 1:

Peter can mow the lawn in 40 minutes and John can mow the lawn in 60 minutes. How long will it take for them to mow the lawn together?

Solution:

Step 1: Assign variables:

Let x = time to mow lawn together

Step 2: Use the formula:

Step 3: Solve the equation

The LCM of 40 and 60 is 120
Multiply both sides with 120

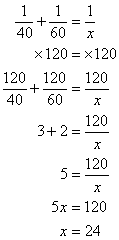
Answer: The time taken for both of them to mow the lawn together is 24 minutes.

“Work” Problems: More than Two Persons

Example 1:

Jane, Paul and Peter can finish painting the fence in 2 hours. If Jane does the job alone she can finish it in 5 hours. If Paul does the job alone he can finish it in 6 hours. How long will it take for Peter to finish the job alone?

Solution:

Step 1: Assign variables:

Let x = time taken by Peter

Step 2: Use the formula:

Step 3: Solve the equation

Multiply both sides with 30x

Answer: The time taken for Peter to paint the fence alone is hours.

“Work” Problems: Pipes Filling up a Tank

Example 1:

A tank can be filled by pipe A in 3 hours and by pipe B in 5 hours. When the tank is full, it can be drained by pipe C in 4 hours. if the tank is initially empty and all three pipes are open, how many hours will it take to fill up the tank?

Solution:

Step 1: Assign variables:

Let x = time taken to fill up the tank

Step 2: Use the formula:

Since pipe C drains the water it is subtracted.

Step 3: Solve the equation

The LCM of 3, 4 and 5 is 60

Multiply both sides with 60

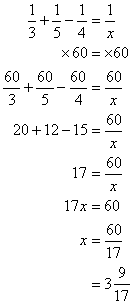
Answer: The time taken to fill the tank is hours.

Custom Search