Basic Algebra Terms
Related Pages
More Algebra Lessons
These lessons introduces basic algebra terms including: constants, variables, coefficients, terms, expressions, equations, quadratic equations and terms in algebraic expressions. These are some algebra vocabulary that will be useful.
The following diagram gives an example to illustrate the following algebra vocabulary that you will need to know: constants, variables, coefficients, terms, expressions, and equations. Scroll down the page for more examples and explanations.
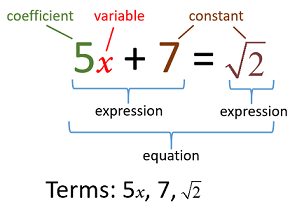
Algebra Worksheets
Practice your skills with the following worksheets:
Printable & Online Algebra Worksheets
Constants
A fixed quantity that does not change. For example: 3, –6, π,
![]()
Variables
A variable is a symbol that we assign to an unknown value. It is usually represented by letters such as x, y, or t. For example, we might say that l stands for the length of a rectangle and w stands for the width of the rectangle.
We use variables when we need to indicate how objects are related even though we may not know the exact values of the objects. For example, if we want to say that the length of a rectangle is 3 times the length of its width then we can write.
l = 3 × w
Coefficients
The coefficient indicates the numerical factor multiplied by a variable in an algebraic term. If a variable stands alone (like x), its coefficient is implicitly 1.
For example, 3 × w can be written as 3w and 3 is the coefficient.
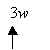
Coefficient
Terms
A term can be any of the following:
- a constant: e.g. 3, 10, π, \(\frac{1}{2}\)
- a single variable
- the product/quotient of numbers and variables: e.g. –3x, 11y, \(\frac{2}{3}a\), x2, xy, 2y2, 7xy
Like Terms
Like terms are terms that differ only in their numerical coefficients. Only like terms can be combined. For example: 3a, 22a,\(\frac{2}{3}\)a.
Expressions
An expression is made up of one or more terms usually separated by addition (+) or subtraction (-) signs. An expression does not contain an equals sign.
For Example:
3w + 4xy + 5
Equations
An equation consists of two expressions separated by an equal sign. The expression on one side of the equal sign has the same value as the expression on the other side.
For Example:
4 + 6 = 5 × 2
l = 3 × w
3w + 4xy + 5 = 2w + 3
Quadratic Equations
A Quadratic Equation is an equation of the form:
ax2 + bx + c = 0, where a, b and c are numbers and a ≠ 0
For Example:
x2 + 2x + 3 = 0
2x2 + 5x – 7 = 0
2x2 + 5x = 8 (is a quadratic equation because it can be changed to 2x2) + 5x – 8 = 0
x2 + x = 0 (is a quadratic with c = 0)
2x2 – 7 = 0 (is a quadratic with b = 0)
2x + 3 = 0 (is not a quadratic because a cannot be 0)
Algebraic Fraction
An algebraic fraction is a fraction that contains an algebraic expression in its numerator and/or denominator. For example: \(\frac{4}{{2x - 3}},\frac{{3x - 5}}{{x + 3}}\)
How to Understand Algebraic Variables
This video will show you how to understand algebraic variables.
In algebra, variables are placeholder letters (capitalized and lowercase) that represent the unknown,
or what you’re solving for. This video shows you what variables can look like and what they mean.
Understanding variables help make algebra easier for you.
How to Understand the Vocabulary Of Algebra
In this video you will learn how to understand the vocabulary of algebra.
Knowing the symbols and expressions used in algebra makes understanding algebra easier. This video explains some common algebra symbols and phrases, such equations, operations, variables, constants, expression, term, equation, operation, variable, constant, exponent, simplify, factor, solve
Differences between an algebraic expression and an algebraic equation
The lesson also explains terms, coefficients and constants.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.