Algebra Work Problems

Work problems are word problems that involve tasks being completed by one or more entities (people, machines, etc.) working at various rates. The problems typically ask you to determine how long it takes to complete a task.

How to solve algebra work problems?

Work Problems are word problems that involve different people or entities doing work together but at different rates. If the people or entities were working at the same rate then we would use the Inversely Proportional Method.

In these lessons, we will learn work problems with pipes filling up a tank and work problems with pumps draining a tank. Look at the related pages above for work problems that involve people.

The following diagram shows the formula for Work Word Problems. Scroll down the page for more examples and solutions for work word problems.

 

Algebra Worksheets
Practice your skills with the following Algebra worksheets:
Printable & Online Algebra Worksheets

The basic formula for work problems is:
Work=Rate×Time
From this, we can derive:
\(Rate=\frac{Work}{Time}\)

In most work problems, the “Work” is defined as completing one whole job. So, if someone takes T hours to complete one job, their rate is
\(R=\frac{1}{T}\) of the job per hour.

Combined Work Formula
When two or more people or machines work together, their individual rates add up to form a combined rate.
If Person A takes T_A time to complete the job alone then their rate is \(R_A = \frac{1}{T_A}\)
If Person B takes T_B time to complete the job alone then their rate is \(R_B = \frac{1}{T_B}\)

When they work together, their combined rate is R_combined = R_A + R_B.
If T_together is the time it takes them to complete the job together, then
R_combined = \(\frac{1}{T_{together}}\)
So, the general formula for two people working together is:
\(\frac{1}{T_{together}}=\frac{1}{T_A}+\frac{1}{T_B}\)

This formula can be extended for any number of workers.

When setting up the equation:
If working together: Add their rates.
If one leaves/joins: Calculate work done individually for specific times, then combine.
If working against each other (like filling/draining): Subtract the rates.

“Work” Problems: Pipes Filling up a Tank

Example 1:
A tank can be filled by pipe A in 3 hours and by pipe B in 5 hours. When the tank is full, it can be drained by pipe C in 4 hours. if the tank is initially empty and all three pipes are open, how many hours will it take to fill up the tank?

Solution:
Step 1: Assign variables:

Let x = time taken to fill up the tank.

Step 2: Use the formula:

Since pipe C drains the water it is subtracted.

Step 3: Solve the equation

The LCM of 3, 4 and 5 is 60

Multiply both sides with 60

 

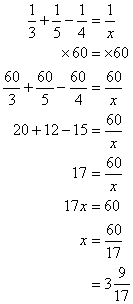
Answer: The time taken to fill the tank is hours.

Work Problem: Pumps draining a tank

Example:
A swimming pool can be emptied in 6 hours using a 10-horsepower pump along with a 6-horsepower pump. The 6-horsepower pump requires 5 hours more than the 10-horsepower pump to empty the pool when working by itself.
How long will it take to empty the pool using just the 10-horsepower pump?

• Show Video Lesson

Cooperative Work Word Problems (Time to Finish)

Examples:

1. Pump A can empty a pool in 20 hours and pump B can empty it in 24 hours. Working together, how long will it take to empty the pool?

2. A painter can paint a building in 15 days and a coworker can do the same job in 10 days. If the first painter starts and 3 days later the coworker joins in to help finish the job, how many days does it take to paint the building?

• Show Video Lesson

Rates of Performing Work Problems

Example:
It takes 12 hours to fill a water tank. It takes 16 hours to drain the same water tank. How long will it take to fill the tank if the drain is left open?

• Show Video Lesson

Check out many other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.