Set Theory: Venn Diagrams And Subsets

Free Roman Numeral Games
Set Operations & Venn Diagrams	Venn Diagram Examples	Set Worksheets

What Is A Venn Diagram?

A Venn Diagram is a pictorial representation of the relationships between sets.

We can represent sets using Venn diagrams. In a Venn diagram, the sets are represented by shapes; usually circles or ovals. The elements of a set are labeled within the circle.

The following diagrams show the set operations and Venn Diagrams for Complement of a Set, Disjoint Sets, Subsets, Intersection and Union of Sets. Scroll down the page for more examples and solutions.

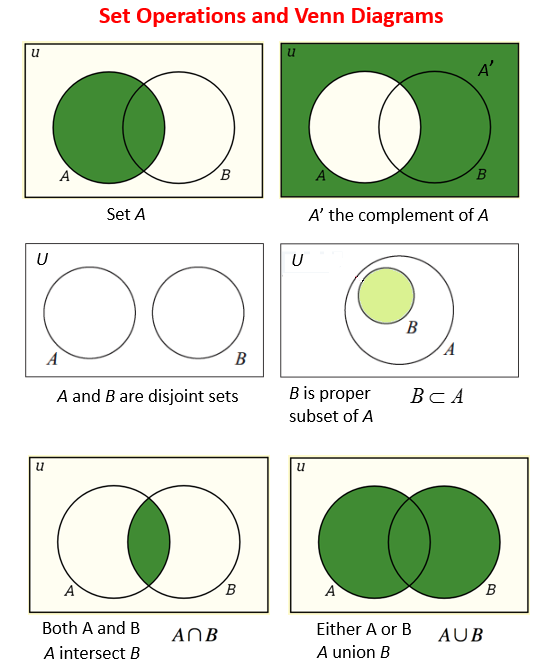
The set of all elements being considered is called the Universal Set (U) and is represented by a rectangle.

• The complement of A, A’, is the set of elements in U but not in A. A’ ={x | x ∈ U and x ∉ A}
• Sets A and B are disjoint sets if they do not share any common elements.
• B is a proper subset of A. This means B is a subset of A, but B ≠ A.
• The intersection of A and B is the set of elements in both set A and set B. A ∩ B = {x | x ∈ A and x ∈ B}
• The union of A and B is the set of elements in set A or set B. A ∪ B = {x | x ∈ A or x ∈ B}
• A ∩ ∅ = ∅
• A ∪ ∅ = A

• Show Video Lesson

Set Operations And Venn Diagrams

Example:
1. Create a Venn Diagram to show the relationship among the sets.
U is the set of whole numbers from 1 to 15.
A is the set of multiples of 3.
B is the set of primes.
C is the set of odd numbers.

2. Given the following Venn Diagram determine each of the following set.
a) A ∩ B
b) A ∪ B
c) (A ∪ B)’
d) A’ ∩ B
e) A ∪ B'

• Show Video Lesson

Venn Diagram Examples

Example:
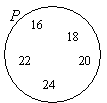
Given the set P is the set of even numbers between 15 and 25. Draw and label a Venn diagram to represent the set P and indicate all the elements of set P in the Venn diagram.

Solution:
List out the elements of P.
P = {16, 18, 20, 22, 24} ← ‘between’ does not include 15 and 25
Draw a circle or oval. Label it P. Put the elements in P.

Example:
Draw and label a Venn diagram to represent the set
R = {Monday, Tuesday, Wednesday}.

Solution:
Draw a circle or oval. Label it R . Put the elements in R.

Example:
Given the set Q = { x : 2x – 3 < 11, x is a positive integer }. Draw and label a Venn diagram to represent the set Q.

Solution:
Since an equation is given, we need to first solve for x.
2x – 3 < 11 ⇒ 2x < 14 ⇒ x < 7

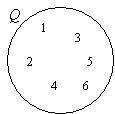
So, Q = {1, 2, 3, 4, 5, 6}
Draw a circle or oval. Label it Q.
Put the elements in Q.

Venn Diagram Videos

What’s a Venn Diagram, and What Does Intersection and Union Mean?

• Show Video Lesson

Venn Diagram and Subsets

Learn about Venn diagrams and subsets.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.