Vector Geometry
In these lessons, we will look at some examples of problems involving vectors in geometrical shapes.
Related Pages
Vectors
Equal Vectors
Negative Vectors
Vector Multiplication
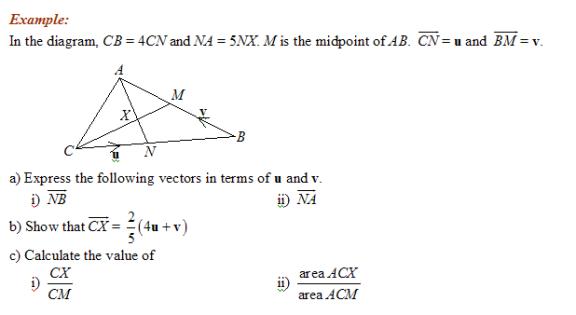
Example:
In the following diagram, 
= u and 
= 2v and
M is the midpoint of *RQ *and N is the midpoint of RM.
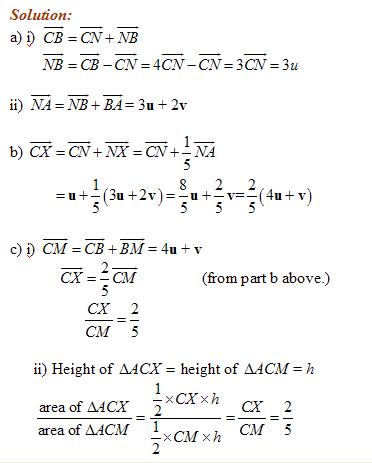
How to solve vector geometry problems?
GCSE Revision Questions on Vectors
Topics in this lesson: Vectors with numbers, magnitude of a vector, algebraic vectors, parallel vectors
Examples:
-
ABCDEF is a regular hexagon.
AB = n
a) Explain why ED = n.
BC = m, CD = p
b) Find (i) AC, (ii) AD
c) What is FD? -
ABC is a straight line where BC = 3AB.
OA = a, AB = b
Express OC in terms of a and b. -
In triangle OAB, OA = a and OB = b.
(i) Find in terms of a and b, the vector AB.
P is the midpoint of AB.
(ii) Find in terms of a and b, the vector AP.
(iii) Find in terms of a and b, the vector OP. -
OABC is a parallelogram with OA = a and OB = b.
E is a point on AC such that AE = 1/4 AC
F is a point on BC such that BF = 1/4 BC.
(a) Find in terms of a and b
(i) AB, (ii) AE, (iii) OE, (iv) OF, (v) EF
(b) Write down two geometric properties connecting EF and AB
Exam Question 1:
AB = 2x and BC = 4y, ABCD is a straight line.
(a) Write down the vector AC in terms of x and y.
(b) AC:CD = 2:1
Works out the vector AD in terms of x and y.
Give your answer as simply as possible.
Exam Question 2:
WXYZ is a trapezium
WX = s, WZ = t, ZY:WX = 3:2
(a) Write vector ZY in terms of s
(b) Work out vector XY in terms of s and t. Give your answer in its simplest form.
Exam Question 3:
PQRS is a trapezium as shown
(a) Write down in terms of a and b vector SR.
(b) Work out in terms of a and b vector QR. Give your answer as simply as possible.
How to do Vectors?
A/A* GCSE Maths revision Higher level worked exam questions (include straight lines)
GCSE Higher maths vector geometry questions including proof of straight and parallel lines grades A/A*.
Vectors on trapeziums, Vectors on triangles, Vectors on rectangles and parallelograms
Geometric Vectors Part 1
This video introduces Geometric Vectors, along with the magnitude, opposite vectors, congruent vectors, and resultants.
- A vector is a quantity that has both magnitude and direction. (It looks like a directed line segment).
- The length of a line segment is the magnitude. The direction indicates the direction of the vector.
- A vector with its initial point at the origin is in standard position.
- The direction of the vector is directed angle between the positive x-axis and the vector.
- If both the initial point and the terminal point are at the origin, it is called a zero vector.
Geometric Vectors with Application Problems
In a rowing exercise, John was rowing directly across a river at the rate of 4 mph.
The current was flowing at a rate of 3 mph. Use a ruler to draw each vector to scale
and draw a vector to represent the path of the boat. Determine the magnitude of the
resultant velocity of the boat by measuring the vector.
A ship leaving port sails for 25 miles in a direction 35° north of due east. Find the magnitude of the vertical and horizontal component.
A piling for a high-rise building is pushed by two bulldozers at exactly the same time.
One bulldozer exert a force of 1550 pounds in a westerly direction. The other bulldozer
pushes the piling with a force of 3050 pounds in a northerly direction.
a. Find the magnitude of the resultant force upon the piling, to the nearest pound.
b. What is the directions of the resultant force upon the piling, to the nearest pound.
Geometric Proofs using Vectors
- Prove the diagonals of a parallelogram meet at right angles if and only if it is a rhombus.
- Prove the midpoints of the sides of a quadrilateral join to form a parallelogram.
- Prove the sum of the squares of the lengths of a parallelogram’s diagonals is equal to the sum of the squares of the lengths of the sides.
- Prove an angle in a semi-circle is a right angle.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.