Sample Space In Probability

The following diagram shows how the sample space for an experiment can be represented by a list, a table, and a tree diagram. Scroll down the page for examples and solutions.

Printable & Online Probability Worksheets

Sample Space

In the study of probability, an experiment is a process or investigation from which results are observed or recorded.

An outcome is a possible result of an experiment.

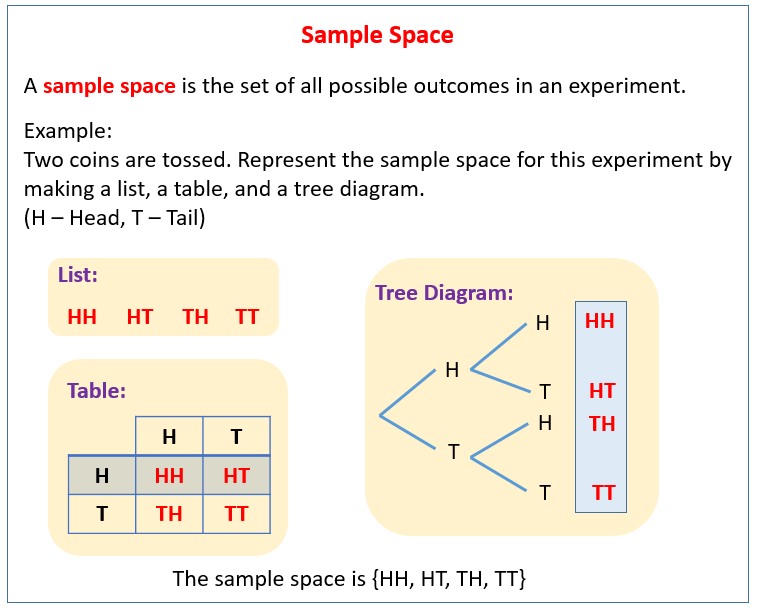
A sample space is the set of all possible outcomes in the experiment. It is usually denoted by the letter S. Sample space can be written using the set notation, { }.

Experiment 1: Tossing a coin
Possible outcomes are head or tail.
Sample space, S = {head, tail}

Experiment 2: Tossing a die
Possible outcomes are the numbers 1, 2, 3, 4, 5, and 6
Sample space, S = {1, 2, 3, 4, 5, 6}

Experiment 3: Picking a card
In an experiment, a card is picked from a stack of six cards, which spell the word PASCAL.
Possible outcomes are P, A ₁, S, C, A ₂ and L.
Sample space, S = {P, A ₁, S, C, A ₂ L}. There are 2 cards with the letter ‘A’

Experiment 4: Picking 2 marbles, one at a time, from a bag that contains many blue and red marbles.
Possible outcomes are: (Blue, Blue), (Blue, Red), (Red, Blue) and (Red, Red).
Sample space, S = {(B,B), (B,R), (R,B), (R,R)}.

A simple explanation of Sample Spaces for Probability

• Show Video Lesson

Sample Space Of An Event

Sample space is all the possible outcomes of an event. Sometimes the sample space is easy to determine. For example, if you roll a dice, 6 things could happen. You could roll a 1, 2, 3, 4, 5, or 6.

Sometimes sample space is more difficult to determine, so you can make a tree diagram or a list to help you figure out all the possible outcomes.

Example 1:
You are ordering pizza. You can choose a small, medium or large pizza and you can choose cheese or pepperoni. What are the possible ways that you could could order a pizza? How many combinations could you have?

Example 2:
Daisy has 3 pairs of shorts, 2 pairs of shoes and 5 t-shirts. How many outfits can she make?

• Show Video Lesson

This lesson is on finding simple probabilities and sample spaces.

Example:
When you roll a die,

1. what is the sample space?
2. P(5)
3. P(Even)
4. P(Prime)
5. P(7)

Example:
Use the spinner below to answer the following questions:

1. What is the sample space?
2. P(Blue)
3. P(Orange or Green)
4. P(Not Red)
5. P(Purple)

• Show Video Lesson

The following video explains simple probability, experiments, outcomes, sample space and probability of an event. It also gives an example of a simple probability problem.

Example:
A jar contains five balls that are numbered 1 to 5. Also, two of the balls are yellow and the others are red. They are numbered and colored as shown below.

1. Find the probability of randomly selecting a red ball.
2. Find the probability of randomly selecting an even number ball.

• Show Video Lesson

Lists and Sample Spaces - Probability

Example:
Entrees - Ribs, Chicken
Sides - Mac and Cheese, Veggies, Mashed Potatoes
Drinks - Water, Coffee, Milk
What are the different possibilities for the menu?

• Show Video Lesson

Explains three methods for listing the sample space of an event and introduces conditional probability: List, Table, Tree Diagram.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.