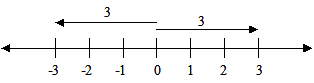Real Numbers - GRE
More Lessons for GRE Math
Math Worksheets
This lesson is part of a series of lessons for the quantitative reasoning section of the GRE revised General Test. In this lesson, we will learn:
- Rational and Irrational Numbers
- Real Numbers
- Inequalities
- Absolute Value
- Properties of Real Numbers
Rational and Irrational Numbers
A rational number is any number that can be expressed as the fraction 
of two integers, with the denominator y not equal to zero. Since y may be equal to 1, every integer is a rational number.
An irrational number is a number that cannot be expressed as a fraction. It is represented by a decimal that does not terminate or repeat.
Examples of irrational numbers are pi(π) = 3.142… and √2 = 1.4142…
Real Numbers
The set of real numbers consists of all rational numbers and all irrational numbers. The real numbers include all integers, fractions, and decimals. The set of real numbers can be represented by a number line called the real number line.
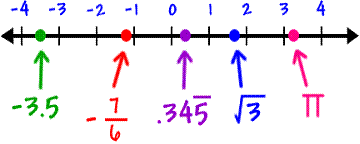
Every real number corresponds to a point on the number line, and every point on the number line corresponds to a real number. On the number line, all numbers to the left of 0 are negative and all numbers to the right of 0 are positive. Only the number 0 is neither negative nor positive.
How to place rational and irrational numbers on the number line?Inequalities
The symbols used for inequality are:> means ‘greater than’
< means ‘less than’
≥ means ‘greater than or equal to’
≤ means ‘less than or equal to’
A real number x is less than a real number y if x is to the left of y on the number line, which is written as x < y.
A real number y is greater than x if y is to the right of x on the number line, which is written as y > x.
For example,
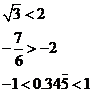
We can use an inequality to represent an interval with one endpoint. For example,
x < 5
x ≤ 5
x > 5
x ≥ 5
We can use a double inequality to represent an interval with two endpoints. For example,
1 < x < 3
1 ≤ x < 3
1 < x ≤ 3
1 ≤ x ≤ 3
The entire real number line is also considered to be an interval
Absolute Value
The absolute value of a number describes the distance of the number on the number line from 0. It does not consider which direction from 0 the number lies. The absolute value of a number is always positive.
The absolute value of 3 is 3 which means that its distance from 0 is 3 units
The absolute value of −3 is also 3 which means that its distance from
0 is 3 units
The symbol for absolute value is two straight lines || (called bars) surrounding
the number or expression for which you wish to indicate absolute value.
| For example: |
| 6 |
= 6 which means the absolute value of 6 is 6. |
| | 3 − 7 | = | −4 | = 4 |
|
| | 6 +
3(−5) | = | 6 − 15 | = | −9 | = 9 |
It is important to note that the absolute value bars do NOT work in the
same way as parentheses. Recall that − (−5) = (−1) × (−5) = +5.
However, for the absolute value it is done by removing the absolute bar
and then performing the sign operation.
−| −5 | = −(+5) = (−1) × (+5)
= −5
Properties of Real Numbers
There are several general properties of real numbers that are used frequently.
The following table gives some properties of real numbers: commutative, associative, distributive, identity, inverse.
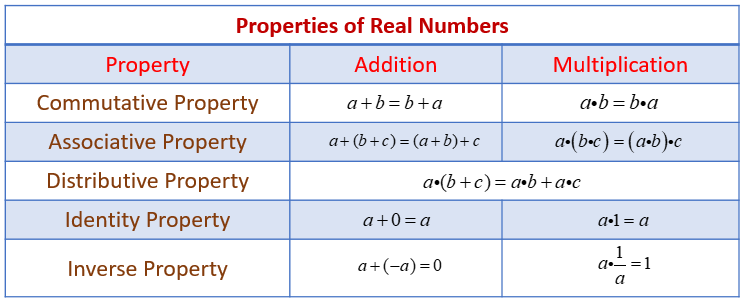
a + b = b + a and ab = ba.
For example, 3 + 5 = 5 + 3 = 8 and (−4)(6) = (6)(−4) = −24
(a + b) + c = a + (b + c) and (ab)c = a(bc).
For example, (8 + 2) + 5 = 8 + (2 + 5) = 15 and (8
) = 8() = 16a (b + c) = ab + ac
For example, 7(4 + 16) = (7)(4) + (7)(16) = 140
a + 0 = a, (a)(0) = 0, and (a)(1) = a
If ab = 0, then either a = 0 or b = 0 or both.
Division by 0 is not defined; for example, 4 ÷ 0, 0 ÷ 0 are undefined.
If both a and b are positive, then both a + b and ab are positive.
If both a and b are negative, then a + b is negative and ab is positive.
If a is positive and b is negative, then ab is negative.
|a + b| ≤ |a| + |b| This is known as the triangle inequality.
|a||b| =|ab|
If a > 1, then a2 > a If 0 < b < 1 then b2 < b, for example,
42 = 16 > 4,
Identity, inverse, commutative, associative and distributive properties and absolute value of real numbers
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.