Decimals - GRE
This lesson is part of a series of lessons for the quantitative reasoning section of the GRE revised General Test. In this lesson, we will learn:
- Decimals, Decimal Place Value, Expanding Decimals
- Convert Decimals to Fractions
- Convert Fractions to Decimals
- Repeating Decimals
- Rational and Irrational Numbers
Decimals
The decimal number system is based on representing numbers using powers of 10. The place value of each digit corresponds to a power of 10.
For example, the digits of the number 7,263.154 have the following place values.
Thousands |
|
Hundreds |
Tens |
Ones |
|
Tenths |
Hundredths |
Thousandths |
7 |
, |
2 |
6 |
3 |
. |
1 |
5 |
4 |
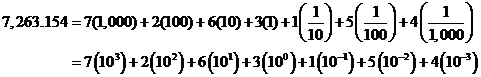
Place values of decimals
How to write a decimal in expanded form with negative powers of ten?
Convert Decimals to Fractions
Since each place value is a power of 10, a decimal can be converted to an integer divided by a power of 10. The fraction can then be reduced to its lowest terms.
For example,
How to change any decimal value into its fraction equivalent in lowest terms?
It also reviews decimal place values in the process and how to reduce to lowest terms.
Convert Fractions to Decimals
Every fraction with integers in the numerator and denominator can be converted to an equivalent decimal by dividing the numerator by the denominator using long division.
For example, To convert 
to a decimal
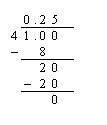
Therefore, = 0.25
How to change any fraction into a decimal?
Repeating Decimals
The decimal that is converted from a fraction will either terminate or the decimal will repeat without end.
Examples of decimals that will terminate.
One way to indicate the repeating part of a decimal that repeats without end is to use a bar over the digits that repeat.
Examples of decimals that will repeat without end.
Rational and Irrational Numbers
A rational number is any number that can be expressed as the fraction 
of two integers, with the denominator y not equal to zero. Since y may be equal to 1, every integer is a rational number.
Since every fraction with integers in the numerator and denominator is equivalent to a decimal that terminates or repeats, every rational number can be expressed as a terminating or repeating decimal. The converse is also true; that is, every terminating or repeating decimal represents a rational number.
An irrational number is a number that cannot be expressed as a fraction. It is represented by a decimal that does not terminate or repeat.
Examples of irrational numbers are
pi(π) = 3.142.. and √2 = 1.4142…
Compare rational and irrational numbers
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.