Calculus - Product Rule

What Is The Product Rule?

The Product Rule is a fundamental rule in calculus, specifically in differential calculus, used to find the derivative of a function that is the product of two or more other differentiable functions.

The Product Rule says that the derivative of a product of two functions is the first function times the derivative of the second function plus the second function times the derivative of the first function.

What Is The Product Rule Formula?

The following image gives the product rule for derivatives. Scroll down the page for more examples and solutions.

 

If you have a function h(x) that is the product of two differentiable functions, say f(x) and g(x): h(x)=f(x)⋅g(x) Then, the derivative of h(x), denoted as h′(x) or \(\frac{d }{dx}\left[ h\left( x \right) \right]\), is given by the formula: \(\frac{d }{dx}\left[ f(x)\cdot g(x) \right]=f’(x)\cdot g(x)+f(x)\cdot g’(x)\)

How To Use The Product Rule?

Example:
Find f’(x) if f(x) = (6x³)(7x⁴)

Solution:
Using the Product Rule, we get

Example:
Given f(x) = (3x² – 1)(x² + 5x +2), find the derivative of f(x).

Solution:
Using the Product Rule, we get

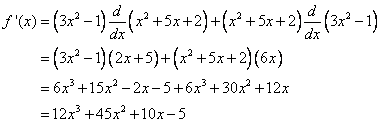
When To Use The Product Rule?

We use the product rule when we need to find the derivative of the product of two functions - the first function times the derivative of the second, plus the second function times the derivative of the first.

The product rule is related to the quotient rule, which gives the derivative of the quotient of two functions, and the chain rule, which gives the derivative of the composite of two functions.

Example:
Find the derivative of f(x) = (3x + 5)(2x² - 3)

• Show Video Lesson

Examples Using The Product Rule And Chain Rule

Find the derivative of

1. f(x) = (5x⁵ - x⁷)(20x² + 3x^-7)
2. f(x) = (10x³ + 5x² - 7)(20x⁸ - 7)
3. y = (x² + 2x)⁵(3x^-3 + x²)^-7

• Show Video Lesson

How To Find Derivatives Using The Product Rule, Chain Rule, And Factoring?

Find the derivative of
f(x) = x⁴(5x - 1)³

• Show Video Lesson

How To Use The Product Rule For Derivatives?

Examples:
Find the derivative of

1. h(x) = (x²)(x³ + 4)
2. (sin x)(cos x)(x² + 1)

• Show Video Lesson

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.