Calculus - Chain Rule

The Chain Rule

The chain rule is a fundamental calculus technique for finding the derivative of composite functions. A composite function is essentially a function within another function. If you have a function \(y = f(g(x))\), the chain rule provides a way to find the derivative of \(y\) with respect to \(x\).

The following figure gives the Chain Rule that is used to find the derivative of composite functions. Scroll down the page for more examples and solutions.

 

The Rule
There are two common ways to express the chain rule:

1. Function Notation:
   If \(h(x) = f(g(x))\), then the derivative of \(h\) with respect to \(x\), denoted as \(h’(x)\), is given by: \( h’(x) = f’(g(x)) \cdot g’(x) \)

2. Leibniz Notation:
   In Leibniz notation, if \(y = f(u)\) and \(u = g(x)\) are both differentiable functions, then
   \( \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} \)

Note: In the Chain Rule, we work from the outside to the inside. We differentiate the outer function and then we multiply with the derivative of the inner function.

Example:
Find the derivatives of each of the following

 

Solution:

 

Example:
Differentiate y = (2x + 1)⁵(x³ – x +1)⁴

Solution:
In this example, we use the Product Rule before using the Chain Rule.

 

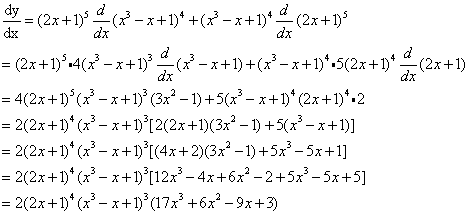
Chain Rule: The General Power Rule

The general power rule is a special case of the chain rule. It is useful when finding the derivative of a function that is raised to the nth power. The general power rule states that this derivative is n times the function raised to the (n-1)th power times the derivative of the function.

This tutorial presents the chain rule and a specialized version called the generalized power rule. Several examples are demonstrated.
Errata: at (9:00) the question was changed from x² to x⁴

• Show Video

Chain Rule: The General Exponential Rule

The exponential rule is a special case of the chain rule. It is useful when finding the derivative of e raised to the power of a function. The exponential rule states that this derivative is e to the power of the function times the derivative of the function.

Derivatives of Exponential Functions. Just some examples of finding derivatives of functions involving exponentials.

• Show Video Lesson

Chain Rule: The General Logarithm Rule

The logarithm rule is a special case of the chain rule. It is useful when finding the derivative of the natural logarithm of a function. The logarithm rule states that this derivative is 1 divided by the function times the derivative of the function.

• Show Video Lesson

Examples using the Chain Rule

• Show Video Lesson

Key Points to Remember

• The chain rule is essential for differentiating composite functions.
• Carefully identify the outer and inner functions.
• Don’t forget to multiply by the derivative of the inner function.
• The chain rule can be applied multiple times for nested composite functions.

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.