Calculus – Derivatives

Related Topics:
More Lessons for Calculus
Math Worksheets



The study of differential calculus is concerned with how one quantity changes in relation to another quantity. The central concept of differential calculus is the derivative.

Definition of Derivative:

The following formulas give the Definition of Derivative. Scroll down the page for more examples and solutions.

Interpretation of the Derivative as the Slope of a Tangent

The tangent line to y = f(x) at (a, f(a)) is the line through (a, f(a)) whose slope is equal to f’(a), the derivative of f at a. This means that the derivative is the slope of a curve at a given point on the curve.

Example:

Use the derivative to find the slope at any point along the following curves.

a) f(x) = 2x²

b) f(x) =

Solution:

a) f(x) = 2x²

b)

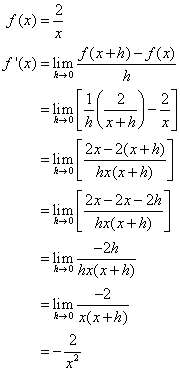
Derivative Notations

If we use the traditional notation y = f(x) to indicate that the independent variable is x and the dependent variable is y, then some common notations for the derivatives are as follows:

What is a derivative?

Understanding the Definition of the Derivative The following video shows how to find the slope of a tangent line to a curve and gives the definition of a derivative. The following video shows how to use the derivative to find the slope at any point along f(x) = x²

• Show Step-by-step Solutions

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.