Inverse Variation Word Problems

The following diagrams show the differences between Direct Variation and Indirect Variation. Scroll down the page for examples and solutions.

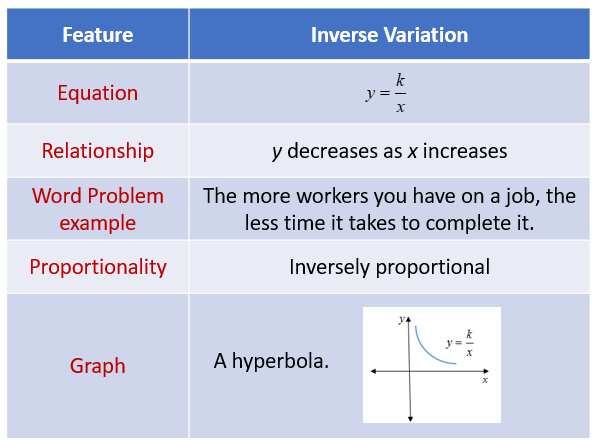
What Is Inverse Variation?

There are many situations in our daily lives that involve inverse variation (indirect variation).

For example, the number of days required to build a bridge varies inversely to the number of workers. As the number of workers increases, the number of days required to build would decrease and as the number of workers decreases, the number of days increases.

Another example would be that speed varies inversely to time. As speed increases, the time taken to cover the same distance decreases and as speed decreases, the time taken increases.

In general, when two variables x and y are such that
xy = k where k is a non-zero constant, we say that y varies inversely with x.

In notation, inverse variation is written as

Example:
Suppose that y varies inversely as x and that y = 8 when x = 3.
a) Form an equation connecting x and y.
b) Calculate the value of y when x = 10.

Solution:
i.e. xy = k where k is a non-zero constant.

a) Substitute x = 3 and y = 8 into the equation to obtain k
3 × 8 = k ⇒ k = 24
The equation is xy = 24

b) When x = 10, 10 × y = 24 ⇒ y =

Example:
Suppose that y varies inversely as x ² and that y = 10 when x = .

a) Find the equation connecting x and y.
b) Find the value of y when x = 3.

Solution:
i.e. yx² = k

a) Substitute x = and y = 10 into the equation to obtain k.

The equation is yx² =

b) When x = 3,

How to define inverse variation and how to solve inverse variation problems?

Examples:

1. y varies inversely as x. y = 4 when x = 2. Determine the inverse variation equation. Then determine y when x = 16.
2. The time, t, required to empty a tank varies inversely as the rate, r, of pumping. If a pump can empty a tank in 2.5 hours at a rate of 400 gallons per minute, how long will it take to empty a tank at 500 gallons per minute?
3. The force, F, needed to break a board varies inversely with the length, L, of the board. If it takes 24 pounds of pressure to break a board 2 feet long, how many pounds of pressure would it take to break a board that is 5 feet long?
4. y varies inversely as the square root of x. y = 6 when x = 16. Determine the inverse variation equation. Then determine y when x = 4.

• Show Video Lesson

How to solve a basic inverse variation problem?

Example:
y varies inversely as x. y = 3 when x = 10. Determine the inverse variation equation. Then determine y when x = 6.

• Show Video Lesson

How to solve an inverse variation problem with a change of variables?

Example:
Given m varies inversely as t, and m = 9 when t = 6, find the variation constant and the inverse variation equation. Then determine m when t = 27.

• Show Video Lesson

How to solve a inverse variation problem when k is a fraction?

Example:
y varies inversely as x. y = 1/2 when x = 2/3. Find the variation constant and the inverse variation equation. Then determine y when x = 2/15.

• Show Video Lesson

What is the difference between direct and inverse variation?

In general, if two quantities vary directly, if one goes up so does the other. If one goes down so does the other.
The following statements are equivalent

• y varies directly as x.
  
• y is directly proportional to x.
  
• y = kx for some constant k.

In general, if two quantities vary indirectly, if one goes up and the other goes down.
The following statements are equivalent

• y varies indirectly as x.
  
• y is inversely proportional to x.
  
• y = k/x for some constant k.

• Show Video Lesson

How to tell if two variables vary inversely or directly?

Recognizing Direct and Inverse Variation

• Show Video Lesson

How to solve direct variation and indirect/inverse variation word problems?

Example:
On a string instrument, the length of a string varies inversely as the frequency of its vibrations. An 11-inch string has a frequency of 400 cycles per second. Find the constant of proportionality and the frequency of a 10-inch string.

• Show Video Lesson

Inverse Variation Equations and Ordered Pairs

This video looks at inverse variation: identifying inverse variations from ordered pairs, writing inverse variation equations, graphing inverse variations, and finding missing values.

Example:
Let x₁ = 4, y₁ = 12 and x₂ = 3. Let y vary inversely as x. Find y₂.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.