Geometry: Congruent Triangles
In these lessons, we will learn
- congruent triangles
- how to tell if triangles are congruent using SSS, SAS, ASA and AAS rules
- why AAA and SSA does not work as congruence shortcuts
- the Hypotenuse Leg Rule for right triangles
- how to use CPCTC (corresponding parts of congruent triangles are congruent)
Related Pages
Congruent Triangles - GCSE
Similar Triangles
Basic Geometry Concepts
More Geometry Lessons
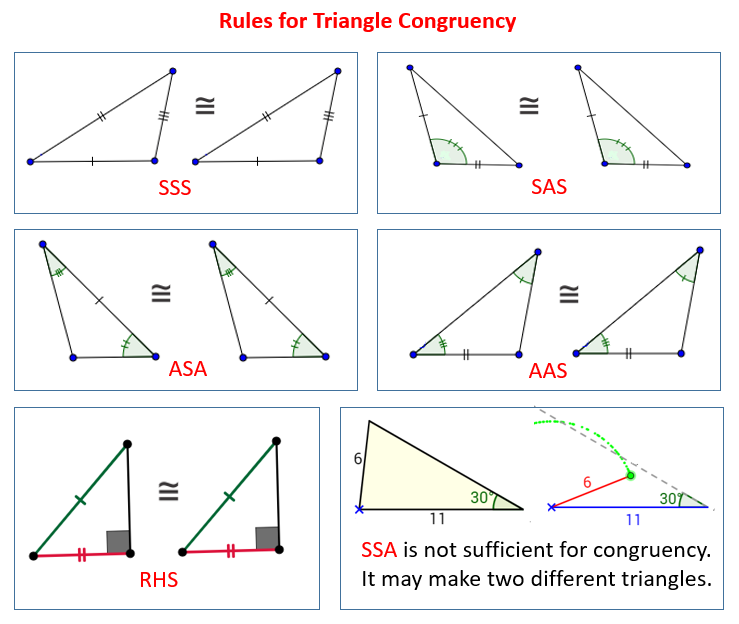
The following diagrams give the rules to determine congruent triangles: SSS, SAS, ASA, AAS, RHS. Scroll down the page for examples and solutions.
Congruent Triangles
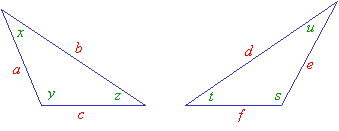
Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.
In the above diagrams, the corresponding sides are a and d; b and e; c and f.
The corresponding angles are x and s; y and t; z and u.
How To Tell If Triangles Are Congruent?
We can tell whether two triangles are congruent without testing all the sides and all the angles of the two triangles. There are four rules to check for congruent triangles. They are called the SSS rule, SAS rule, ASA rule and AAS rule. There is also another rule for right triangles called the Hypotenuse Leg rule. As long as one of the rules is true, it is sufficient to prove that the two triangles are congruent.
SSS Rule
The Side-Side-Side (SSS) rule states that
If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.
SAS Rule
The Side-Angle-Side (SAS) rule states that
If two sides and the included angle of one triangle are equal to two sides and included angle of another triangle, then the triangles are congruent.
An included angle is the angle formed by the two given sides.
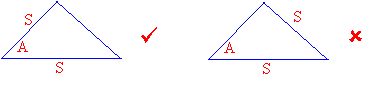
Included Angle Non-included angle
ASA Rule
The Angle-Side-Angle (ASA) Rule states that
If two angles and the included side of one triangle are equal to two angles and included side of another triangle, then the triangles are congruent.
An included side is the side between the two given angles.
AAS Rule
The Angle-Angle-Side (AAS) Rule states that
If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent.
(This rule may sometimes be referred to as SAA).
For the ASA rule the given side must be included and for AAS rule the side given must not be included. We must use the same rule for both the triangles that we are comparing.
Compare AAS with AAS
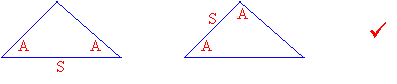
Compare ASA with ASA
Compare AAS with ASA
How to determine whether given triangles are congruent, and to name the postulate that is used?
If the three sides of one triangle are congruent to the three sides of another triangle,
then the triangles are congruent (Side-Side-Side or SSS).
If two sides and the included
angle of one triangle are congruent to two sides and the included angle of another triangle,
then the triangles are congruent (Side-Angle-Side or SAS).
If two angles and the
included side of one triangle are congruent to two angles and the included side of another
triangle, then the triangles are congruent (Angle-Side-Angle or ASA).
Explain the rules: SSS, SAS, ASA, AAS
Present two column proofs using the rules.
Example:
Which of the following conditions would be sufficient for the above triangles to be congruent?
a) a = e, x = u, c = f
b) a = e, y = s, z = t
c) x = u, y = t, z = s
d) a = f, y = t, z = s
Solution for a):
Step 1: a = e gives the S
x = u gives the A
c = f gives the S
Step 2: Beware! x and u are not the included angles. This is not SAS but ASS which is not one of the rules. Note that you cannot compare donkeys with triangles!
Answer for a): a = e, x = u, c = f is not sufficient for the above triangles to be congruent.
Solution for b):
Step 1: a = e gives the S
y = s gives the A
z = t gives the A
Step 2: a and e are non-included sides. Follows the AAS rule.
Answer for b): a = e, y = s, z = t is sufficient show that the above are congruent triangles.
Solution for c):
Step 1: x = u gives the A
y = t gives the A
z = s gives the A
Step 2: AAA is not one of the rules.
Answer for c): x = u, y = t, z = s is not sufficient for the above triangles to be congruent.
Solution for d):
Step 1: a, y, z follows AAS (non-included side)
f ,t, s follows the ASA (included side)
Step 2: Comparing AAS with ASA is not allowed
Answer for c): a = f, y = t, z = s is not sufficient to show that the above are congruent triangles.
Why SSA and AAA Don’t Work as Congruence Shortcuts
AAA Does not Work Triangles with all three corresponding angles equal may not be congruent. These triangles will have the same shape but not necessarily the same size. They are called similar triangles.
SSA Does not Work Triangles with two corresponding sides and one non-included angle equal may not be congruent.
SSA Can’t Be Used to Prove Triangles are Congruent
This video explains why there isn’t an SSA Triangle Congruence Postulate or Theorem.
Congruence Theorems - AAA, SSA
Now that we know 4 ways to prove two triangles are congruent, lets look at two non-congruence theorems.
Students often use these to prove triangles are congruent which is incorrect.
Hypotenuse Leg Rule
The Hypotenuse-Leg (HL) Rule states that
If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.
In the right triangles ΔABC and ΔPQR , if AB = PR, AC = QR then ΔABC ≡ ΔRPQ .
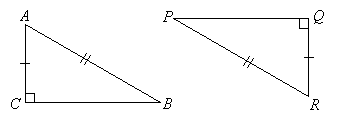
How to use the Hypotenuse - Leg Congruence Theorem?
CPCTC
CPCTC stands for Corresponding Parts of Congruent Triangles are Congruent.
CPCTC states that
If two or more triangles are proven congruent by: ASA, AAS, SSS, HL, or SAS, then all of their corresponding parts are congruent as well. This can be used to prove various geometrical problems and theorems.
CPCTC Triangle Congruence
The following video shows how to use the principle that corresponding parts of congruent triangles
are congruent, or CPCTC.
How do we use congruent triangles to prove line segments or angles congruent?
Proving triangles are congruent using their corresponding parts.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.