Algebra: Coin Word Problems
Related Pages
Word Problems Involving Age
Ticket Word Problems
More Algebra Lessons
In these algebra lessons, we will discuss coin problems, which is a category of word problems that involve pennies, nickels, dimes, quarters or half dollars. Examples and solutions are shown to help you learn how to solve this type of word problems.
Be careful to distinguish between the value of the items and the quantity of the items. A table is useful for distinguishing between quantity and value in coin problems.
It is useful to learn how to solve coin problems as we commonly handle these items in everyday life.
Other similar algebra word problems may involve items with specific values like stamps or tickets. Examples and solutions of these are shown in Stamp Problems and Ticket Problems.
Problems Involving Coins
Steps for Solving Coin Problems:
- Define variables for the number of each type of coin.
- Set up equations based on:
The total number of coins.
The total value of the coins.
Any additional relationships (e.g., “twice as many”). - Solve the equation or system of equations.
- Check the solution to ensure it makes sense in the context of the problem.
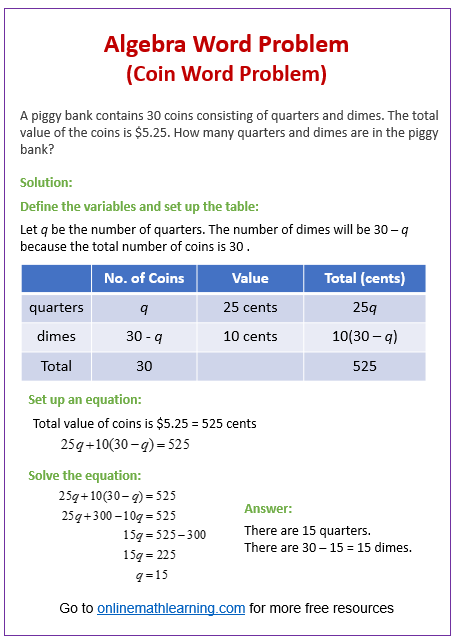
The following diagram shows how to solve a coin word problem. Scroll down the page for more examples and solutions.
Example 1:
Jane bought a pencil and received change for $3 in 20 coins, all nickels and quarters.
How many of each kind are given?
Solution:
Step 1: Set up a table with quantity and value.
| quantity | value | total | |
|---|---|---|---|
| nickels | |||
| quarters | |||
| together |
Step 2: Fill in the table with information from the question.
Jane bought a pencil and received change for $3 in
20 coins, all nickels and quarters.
Let n = number of nickels
q = number of quarters
Total = quantity × value
| quantity | value | total | |
|---|---|---|---|
| nickels | n | 5¢ | 5n |
| quarters | q | 25¢ | 25q |
| together | 20 | 300¢ |
Step 3: Add down each column to get the equations
n + q = 20 (equation 1)
5n + 25q = 300 (equation 2)
Use Substitution Method
Isolate variable n in equation 1
n = 20 – q (equation 3)
Substitute equation 3 into equation 2
5(20 – q) + 25q = 300
100 – 5q + 25q = 300
25q – 5q = 300 – 100
20q = 200
q = 10
Substitute q = 10 into equation 1
n + 10 = 20
n = 10
Answer: Jane received 10 nickels and 10 quarters.
Example 2:
John received change worth $13. He received 10 more dimes than nickels and 22 more quarters than dimes.
How many coins of each did he receive?
Solution:
Step 1: Set up a table with quantity and value.
| quantity | value | total | |
|---|---|---|---|
| nickels | |||
| dimes | |||
| quarters | |||
| together |
Step 2: Fill in the table with information from the question.
John received change worth $13. He received 10 more dimes than nickels and 22 more quarters than dimes.
Let d = number of dimes.
From the question, work out the relationship between dimes and the other types of coins.
nickels = dimes – 10 = d – 10
quarters = dimes + 22 = d + 22
Total = quantity × value
| quantity | value | total | |
|---|---|---|---|
| nickels | d – 10 | 5¢ | 5(d – 10) |
| dimes | d | 10¢ | 10d |
| quarters | d + 22 | 25¢ | 25(d + 22) |
| together | 1300¢ |
Step 3: Add down the total column to get the equation
5(d – 10) + 10d + 25(d + 22) = 1300
Use Distributive Property and
Combine Like Terms
5d – 50 + 10d + 25d + 550 = 1300
5d + 10d + 25d = 1300 + 50 – 550
40d = 800
d = 20
nickels = d – 10 = 10
quarters = d + 22 = 42
Answer: John received 10 nickels, 20 dimes and 42 quarters.
Example:
Martin has a total of 19 nickels and dimes worth $1.65. How many of each type of coin does he have?
Example:
Jim has quarters and nickels. He has twice as many quarters as nickels. If the value of the
coins totals $4.40, how many quarters and nickels does Jim have?
This video gives an example of using an equation to solve a problem involving coins.
Problem:
Zach had $11.85 in his piggy bank. He only had nickels and quarters in the bank. The number of
quarters is equal to one less than twice the number of nickels. How many of each kind of coin did he have?
Solving for an unknown number of coins given the total number of coins and the type of coins.
Problem:
Lucy saves all of her quarters and dimes in a jar. She collected 170 coins that are worth $26.
How many of each coin does she have?
This video shows how to solve a word problem having to do with different coins and their values. This is solved with one variable, but more than one coin is defined. It is done with a chart.
Example:
Barb has $1.15 in her wallet, which contains 18 coins in nickels and dimes. Find how many of
each kind coin she has in her wallet.
Have a look at the following video for another example:
A mixture-type word problem (coins)
One of the easiest of all the mixture word problems to understand is the coin problem since all
students have some understanding of coins.
Example:
In a collection of dimes and quarters there are 6 more dimes than quarters. If there is $29.65
overall, how many of each are there?
Check out many other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.