Circle Theorems
Related Pages
Angles In A Circle
Tangents Of Circles And Angles
Circles
More Geometry Lessons
In these lessons, we will learn:
- inscribed angles and central angles.
- a circle theorem called The Inscribed Angle Theorem or The Central Angle Theorem or The Arrow Theorem.
- how to prove the Inscribed Angle Theorem.
The following diagram shows some examples of Inscribed Angle Theorems. (Click on the diagram to get a printable (pdf) document). Scroll down the page for more examples and solutions on how to use the Inscribed Angle Theorems.
Inscribed Angles and Central Angles
We will first look at some definitions.
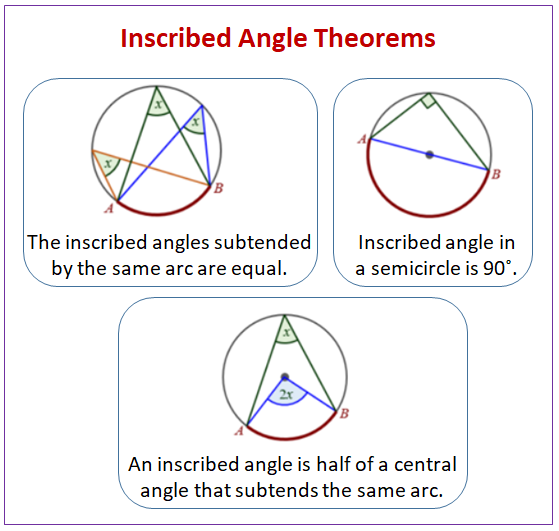
An inscribed angle has its vertex on the circle. ∠ABC, in the diagram below, is called an inscribed angle or angle at the circumference. The angle is also said to be subtended by (i.e. opposite to) arc ADC or chord AC.
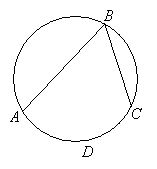
Property: The inscribed angles subtended by the same arc are equal.
∠x = ∠y because they are subtended by the same arc AEC.
Property: Inscribed angle in a semicircle is 90
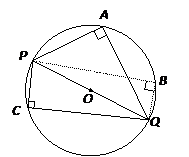
POQ is the diameter. ∠PAQ = ∠PBQ = ∠PCQ = 90˚.
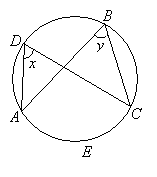
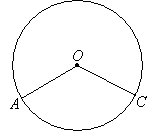
A central angle has its vertex is at the centre of the circle. In the diagram below, ∠AOC is called a central angle.
Property: Central angles subtended by arcs of the same length are equal.
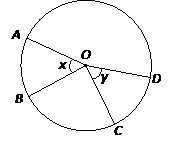
∠ x = ∠ y because arc AB = arc CD
Inscribed angles and central angles
How to use the properties of inscribed angles and central angles to find missing angles?
(1) Central angles subtended by arcs or chords of the same length are equal.
(2) If two inscribed angles subtend the same arc or chord, then the angle measures are equal.
Central angles and inscribed angles that relate to circles
A central angle has its vertex is the middle of the circle.
An inscribed angle has one endpoint on the edge of the circle and then cuts across the rest of the circle. The vertex of its angle is on the circumference.
Any inscribed angle that ends on the same two points has the same measure unless the vertex is on the minor arc. If their vertices are on opposite arcs then they are supplementary.
Any inscribed angle whose endpoints are a diameter is a right angle, or 90 degree angle.
The Central Angle Theorem states that the inscribed angle is half the measure of the central angle. In this video, we can see that the purple inscribed angle and the black central angle share the same endpoints. If the inscribed angle measure x, the central angle will measure 2x. For example, if the central angle is 90 degrees, the inscribed angle is 45 degrees.
Inscribed Angle Theorem
Now, we will look at the Inscribed Angle Theorem. It is also called the Central Angle Theorem or Arrow Theorem.
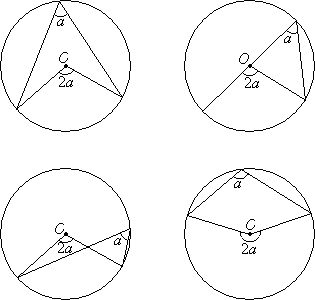
The theorem states
The measure of the central angle is equal to twice the measure of the
inscribed angle subtended by the same arc.
or
An inscribed angle is half of a central angle that subtends the same arc.
or
The angle at the centre of a circle is twice any angle at the circumference subtended by the same arc.
The following diagrams illustrates the Inscribed Angle Theorem.
Example:
The center of the following circle is O. BOD is a diameter of the circle. Find the value of x.
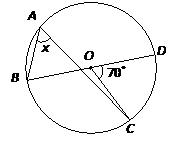
Solution:
∠BOC + 70˚ = 180˚
∠BOC= 110˚
2x = 110˚
x = ![]() × 110˚
× 110˚
= 55˚
Circle Theorem
Basic definitions: Chord, segment, sector, tangent, cyclic quadrilateral.
Theorem: Angle subtended at the centre of a circle is twice the angle at the circumference.
Central Angle Theorem and how it can be used to find missing angles
It also shows the Central Angle Theorem Corollary:
The angle inscribed in a semicircle is a right angle.
How to solve problems involving angles inscribed in circles
Proof of the Inscribed Angle Theorem
This video proves the theorem that an inscribed angle is half of a central angle that subtends the same arc.
Proof of Central Angle Theorem (which would also proof the Inscribed Angles Theorem)
The central angle is twice the inscribed angle that subtends the same arc.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.