Area Of Circles
Related Pages
Geometry: Circles
Angles In A Circle
Conic Sections: Circles
In these lessons, we will learn
- the formula for the area of a circle
- how to find the area of a circle given radius or diameter,
- how to solve word problems using the area of a circle,
- when given the area, how to find the radius or diameter,
- when given the area, how to find the circumference,
- how to prove the formula for the area of a circle.
Area of a Circle
The area of a circle is the amount of space enclosed within its circumference.
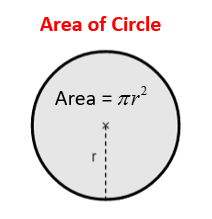
The formula for the area (A) of a circle is:
A = πr2
Where:
A = Area of the circle.
π (pi) is a mathematical constant, approximately 3.14159.
r = radius of the circle.
The following diagram gives the formula for the area of a circle. Scroll down the page for more examples and solutions on how to use the formula and also a proof or the formula.
What if you don’t have the radius?
If you are given the diameter (d): Divide the diameter by 2 to get the radius: \(r = \frac{d}{2} \).
If you have the circumference (C): The circumference is C = 2πr. Solve for r to get \( r = \frac{C}{2π} \).
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
Proof for the Formula of a Circle
While a rigorous mathematical derivation involves calculus, you can intuitively understand the formula by imagining “unrolling” a circle:
The following diagram shows a visual proof for the formula of the area of a circle.
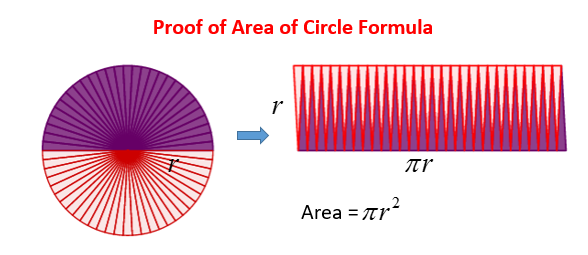
How the Area is Derived (Conceptual Understanding)
- Imagine cutting a circle into many very thin, equal sectors (like slices of a pizza).
- Arrange these slices side-by-side, alternating the direction of the pointed ends.
- Form a Rectangle (Approximate): As you cut the circle into more and more slices, the arrangement starts to resemble a rectangle.
The “height” of this approximate rectangle would be the radius (r) of the original circle.
The “length” of this approximate rectangle would be roughly half the circumference (C) of the original circle, because half the curved edges are on
the top and half are on the bottom. So, the length is approximately \(\frac{1}{2} C\) - We know the circumference C=2πr. So, the “length” of the rectangle is \(\frac{1}{2}(2πr) = πr\)
- The area of a rectangle is length × height. Area ≈ (πr) × r = πr2
As the number of slices approaches infinity, this approximation becomes exact, yielding the formula A = πr2
Formula for the Area of a Circle
A circle is a closed curve formed by a set of points on a plane that are the same distance from its center. The area of a circle is the region enclosed by the circle. The area of a circle is equals to pi (π) multiplied by its radius squared.
Pi (π) is the ratio of the circumference of a circle to its diameter. Pi is always the same number for any circle. The value of π (pi) is approximately 3.14159265358979323846… but usually rounding to 3.142 should be sufficient.
The area of a circle is given by the formula:
A = πr2 (see
a mnemonic for this formula)
where A is the area and r is the radius.
Since the formula is only given in terms of radius, remember to change from diameter to radius when necessary. The radius is equals to half the diameter.
Area of a circle given the diameter or radius
Example 1:
Find the area the circle with a diameter of 10 inches.
Solution:
| Step 1: Write down the formula: | A = πr2 |
| Step 2: Change diameter to radius: | |
| Step 3: Plug in the value: | A = π52 = 25π |
Answer: The area of the circle is 25π ≈ 78.55 square inches.
Example 2:
Find the area the circle with a radius of 10 inches.
Solution:
| Step 1: Write down the formula: | A = πr2 |
| Step 2: Plug in the value: | A = π102 = 100π |
Answer: The area of the circle is 100π ≈ 314.2 square inches.
See also:
Area of a Sector
Worksheet to calculate the area of circle
Worksheet to calculate circumference and area of circle when given diameter or radius
How to use the formula A = πr2 to calculate the area of the circle given the radius?
Example:
Find the area of a circle with radius 4cm.
How to use the formula to calculate the area of the circle given the radius or the diameter?
Example:
- Find the area of a circle with radius 3cm.
- Find the area of a circle with diameter 20cm.
Word Problems using area of circles
The following videos show how to solve word problems using the area of circles.
Example:
There are two circles such that the radius of the larger circle is three times the radius of the smaller circle.
(a) How many times the circumference of the larger circle is the circumference of the smaller circle?
(b) What is the ratio of the area of the larger circle to the area of the smaller circle?
Area and Circumference Word Problems
Example 1: Janell wants to replace the glass in her mirrors. She can buy glass for $0.89 per square inch. If the price includes tax, how much would she pay, to the nearest penny?
Example 2: The rectangle has a length of 21 inches and each circle is congruent. What is the area of one circle?
Example 3: A tire from Karen’s car is shown below. What is the closest distance traveled, in feet, after 3 full rotations of the tire?
Find radius or diameter of a circle when given the area
From the formula A = πr2, we see that we can find the radius of a circle by
dividing its area by π and then get the positive square-root. The diameter is then twice the radius.
This video shows how to find the radius or diameter of a circle when given the area.
Examples:
The area of a circle is 12.56 yd2. What is the circle’s diameter? (take π = 3.14)
Find the circumference of a circle, given the area
Worksheet to calculate problems that involve the radius, diameter, circumference and area of circle
Worksheet on word problems that involve circles 1
Worksheet on word problems that involve circles 2
To find the circumference of a circle when given the area, we first use the area to find the radius. Then, we use the radius to find the circumference of the circle.
How to find the circumference of a circle given the area?
Example:
The area of the circle is 12.56 cm2. What is the circle’s circumference?
How to calculate areas of circles and also composite shapes with circles or segments of circles?
The shape is made from 4 semicircles of diameter 8m and a square of side 8m. The radius of each circle is therefore 4m, and you have the equivalent of 2 whole circles. Then add on the area of the square.
Graphical proof of the formula of a circle
It involves dividing the circle into many sectors and rearranging the sectors to form
a rectangle. The base of the rectangle is shown to be πr and the height of the
rectangle is r. The area of the rectangle is then the product of πr and r. The
area of the circle which is equal to area of the rectangle is then πr2.
Area of Circle Calculator
Enter the radius and this area of circle calculator will give you the area. Use it to check your answers.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.