Solving Systems Of Equations Using The Addition Method (Opposite-Coefficients Method)

Related Pages
Solving Equations
Worksheet: Solving Systems Of Equations By Addition
More Algebra Lessons

The following steps show how to solve a System of Equations using the Addition or Elimination Method. Scroll down the page for examples and solutions.

In some word problems, we may need to translate the sentences into more than one equation. If we have two unknown variables then we would need at least two equations to solve the variable. In general, if we have n unknown variables then we would need at least n equations to solve the variable.

There are two main methods to use when you need to solve more than one equation: Substitution Method and Addition Method.

Check the coefficients"> of the variables. If the coefficient of one of the variables is 1 then use the Substitution Method otherwise use the Addition Method.

In the Addition Method, the two equations are added together to eliminate one of the variables. We try to get the coefficients of one of the variables to be opposites so that addition will eliminate it.

Let’s look at some examples for this free algebra tutorial.

Example 1:
2x + 3y = –2      (equation 1)
4x – 3y = 14      (equation 2)

Solution:

Step 1: In this example the coefficients of y are already opposites (+3 and –3). Just add the two equations to eliminate y.

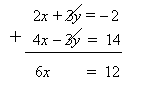
Step 2: Isolate variable x
6x = 12

Step 3: To get the value of y you need to use the substitution method. Substitute x = 2 into <class=“highlight-label”> equation 1.
2(2) + 3y = –2
4 + 3y = –2

Step 4: Isolate variable y
3y = –6
y = –2

Step 5: Check your answer with <class=“highlight-label”> equation 2
4(2) – 3(–2) = 8 – (–6) = 8 + 6 = 14

Answer: x = 2 and y = –2

Example 2:
2x + 3y = 1        (equation 1)
3x – 4y = 10      (equation 2)

Solution:

Step 1: In this example none of the coefficients are opposites. We need to multiply the equations with some numbers to get the coefficients opposite. Lets take the coefficients of y.

Multiply each term of <class=“highlight-label”> equation 1 by 4
8x + 12y = 4

Multiply each term of <class=“highlight-label”> equation 2 by 3
9x – 12y = 30

Step 2: Add the two equations to eliminate y.

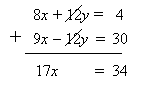
Step 3: Isolate variable x
17x = 34

Step 4: To get the value of y you need to use the substitution method. Substitute x = 2 into <class=“highlight-label”> equation 1.
2(2) + 3y = 1
4 + 3y = 1

Step 5: Isolate variable y
3y = –3
y = –1

Step 6: Check your answer with <class=“highlight-label”> equation 2
3(2) – 4(–1) = 6 – (–4) = 6 + 4 = 10

Answer: x = 2 and y = –1

How to use the addition (Elimination) Method to solve a system of linear equations?

Step 1: “Line up” the variables.
Step 2: Determine which variable to eliminate. Make the coefficients opposites.
Step 3: Add straight down. (One variable should be eliminated.)
Step 4: Solve the resulting equation.
Step 5: Substitute this result into either of the original equations.
Step 6: Solve for the variable to find the ordered pair solution.
Step 7: Check the solution in both originals equations.

Examples:

1. Solve the system of equations using the Addition (Elimination) Method
   4x - 3y = -15
   x + 5y = 2
   
2. Solve the system of equations using the Addition (Elimination) Method
   3x - 2y = -12
   5x - 8y = 8
   
3. Solve the system of equations using the Addition (Elimination) Method
   7x - 2y = 41
   3x - 5y = 1
   

• Show Video Lesson

Solving a system of equations using the elimination (addition) method

This example requires multiplying one equation by a constant.
3x + y = -10
7x + 5y = -18

• Show Video Lesson

System of Equations Using Elimination (No Solution)

5x + 2y = 4
5x + 2y = -2

• Show Video Lesson

System of Equations Using Elimination (Infinite Solutions)

2x - 5y = 4
2x = 5y + 4

• Show Video Lesson

Systems of Equations Calculator

This tool will help you check your steps and answers when solving two equations in two variables.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.