Vertical Angles
Related Pages
Angles
Pairs Of Angles
Types Of Angles
More Geometry Lessons
In these lessons, we will learn
- how to identify vertical angles,
- the vertical angle theorem,
- how to solve problems involving vertical angles,
- how to proof vertical angles are equal.
Vertical Angles
In geometry, pairs of angles can relate to each other in several ways. When two lines intersect, they form four angles. The opposite angles form vertical angles or vertically opposite angles. They are called vertical angles because they share the same vertex.
The Vertical Angle Theorem states that
Vertical angles are equal.
The following diagram shows the vertical angles formed from two intersecting lines. Scroll down the page for more examples and solutions.
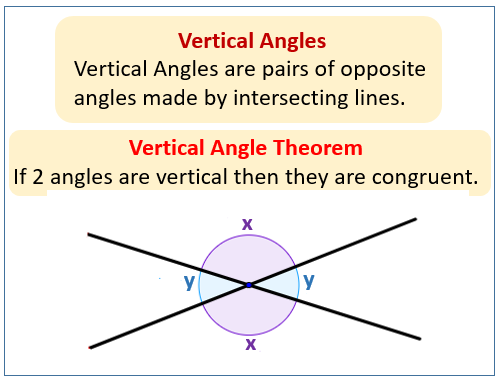
Notice also that x and y are supplementary angles i.e. their sum is 180°.
Geometry Worksheets
Practice your skills with the following geometry worksheets:
Printable & Online Geometry Worksheets
The following diagram shows another example of vertical angles.
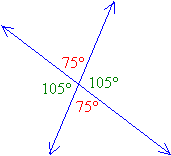
The following video explains more about vertical angles.
How to define and identify vertical angles?
A group of examples that identifies vertical angles.
Solving Problems using Vertical Angles
Very often math questions will require you to work out the values of angles given in diagrams by applying the relationships between the pairs of angles.
Example:
Given the diagram below, determine
the values of the angles x, y and z.
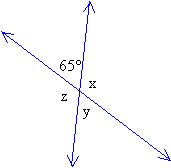
Solution:
Step 1: x is a supplement of 65°.
Therefore, x + 65° = 180° ⇒ x = 180° 65° = 115°
Step 2: z and 115° are vertical angles.
Therefore, z = 115°
Step 3: y and 65° are vertical angles.
Therefore, y = 65°
Answer: x = 115°, y = 65° and z = 115°
Example:
Both AEC and DEB are straight lines. Find q.
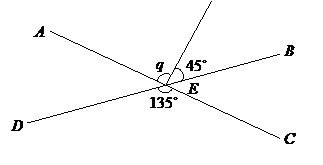
Solution:
∠AEB = ∠DEC ← vertical angles
q + 45˚= 135˚
q = 135˚ – 45˚ = 90˚
The following video shows how to find a missing vertical angle in a triangle.
Proof of the Vertical Angle Theorem
The following videos will prove that vertical angles are equal.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.