Magnitude of a Vector

Magnitude of a Vector

The magnitude of a vector (or modulus of a vector) is a scalar quantity that represents its length or size. It tells you “how much” of a quantity the vector represents, without regard to its direction.

Think of a vector as an arrow pointing from a starting point to an ending point. The magnitude is the length of that arrow

The following diagram shows how to find the magnitude of a 2-D vector. Scroll down the page for more examples and solutions to calculate the magnitudes of 2-D and 3-D vectors.

 

The following diagram shows how to find the magnitude of a 3-D Vector.

 

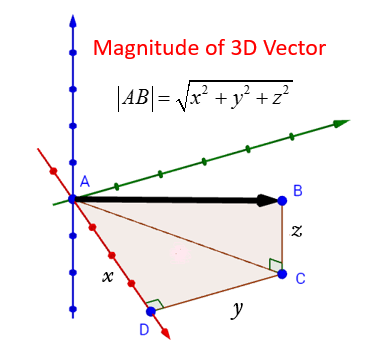
How to Calculate the Magnitude of a Vector
The formula for the magnitude of a vector is derived from the Pythagorean theorem, as a vector’s components can be thought of as the legs of a right triangle, and the magnitude is its hypotenuse.

1. In Two Dimensions (2D)
   If a vector v has components (x,y), its magnitude is calculated as:
   \(\left| v \right|=\sqrt{x^{2}+y^{2}}\)
   
   Example: Find the magnitude of vector \textbf{v}=\left( 3,4 \right)
   \(\left| v \right|=\sqrt{3^{2}+4^{2}}=5\)

2. In Three Dimensions (3D)
   If a vector v has components (x,y,z), its magnitude is calculated as:
   \(\left| v \right|=\sqrt{x^{2}+y^{2}}+z^{2}\)
   
   Example: Find the magnitude of vector \(\textbf{w}=\left( 2,-3,6 \right)\)
   \(\left| w \right|=\sqrt{2^{2}+(-3)^{2}+6^{2}}=7\)
   

Example (2D vector):
Express each of the following vectors as a column vector and find its magnitude.

 

Key characteristics of magnitude:

1. It is always a non-negative value (either positive or zero). A magnitude of zero means the vector is a “zero vector” (a point).
2. It is a scalar quantity, meaning it has no direction.
3. It is often denoted by double vertical bars around the vector symbol, like ||v|| or single vertical bars, |v|.

Videos

Vectors in 2D

Adding vectors geometrically, scalar multiplication, how to find the magnitude and direction angle of a vector.
A vector with initial point at the origin and terminal point at (a, b) is written <a, b>.
Geometrically, a vector is a directed line segment, while algebraically it is an ordered pair.

Example:
Find the magnitude and the direction angle for u = <-3, 4>

• Show Video Lesson

Vectors: magnitude of a vector in 2D.

Example:
Find the magnitude of the following vectors:
a = 4i - 3j
b = -2i + 5j

• Show Video Lesson

Vectors in 3D

A vector can also be 3-dimensional.
The following video gives the formula, and some examples of finding the magnitude, or length, of a 3-dimensional vector.

Example:
Find the magnitude:
a = <3, 1, -2>
b = 5i -j + 2k

• Show Video Lesson

Vectors : Magnitude of a vector 3D.

Examples:

1. Find the magnitude of a = 4i + 3j + 2k
2. If A(3, -5, 6) and B(4, 1, 3) find the length AB.

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.