Trig Graph Game

Trig Graph Quiz/Game
This game will show you a trigonometric graph, and you must identify the correct function (Sine, Cosine, Tangent, and their reciprocals, Cosecant, Secant and Cotangent). Scroll down the page for a more detailed explanation.
 

 
Analyze the Wave:

How to Play

1. Analyze the Wave:
   Look at where the yellow line starts, where it crosses the center axis (the x-axis), and if it has any “gaps” (asymptotes).
   
2. Pick Your Answer:
   Select on of the functions.
   
3. Select the Match:
   Click one of the four buttons.
   Green Flash: You matched correctly
   Red Flash: You missed it. The game will immediately highlight the correct answer in green so you can memorize it for the next round.
   
4. Next Question: Click the Next Question button to generate a brand-new random graph.
5. Scoring and Content
   The game tracks your progress in the top-left corner (Score: Correct / Total Attempts).
    
   

How to remember the Trig Graphs
The Continuous Waves: Sine and Cosine
These are the most common graphs. They oscillate perfectly between a maximum of 1 and a minimum of -1.
Sine (y = sin x): This is an odd function. Passes exactly through the origin (0,0), moves up to its peak at π/2, and crosses the x-axis again at π.
Cosine (y = cos x): This is an even function. It starts at its maximum value (0,1), crosses the x-axis at π/2, and hits its minimum at π.

The Asymptotic Vines: Tangent and Cotangent
These functions involve division by zero at certain points, creating asymptotes. Their range is (-∞, ∞).
Tangent (y = tan x): This function “climbs” from left to right. It passes through the origin (0,0) and has asymptotes at x = ± π/2.
Cotangent (y = cot x): This is the mirror-opposite; it “falls” from left to right. It has asymptotes at x = 0 and x = π.

The Reciprocal Cups: Cosecant and Secant
These graphs look like a series of “U” shapes (parabolas) that never enter the space between -1 and 1. They “sit” on the peaks and valleys of Sine and Cosine.
Cosecant (y = csc x): The reciprocal of Sine (1/sin x). Wherever Sine is 0, Cosecant has an asymptote. Its “cups” touch the Sine wave at its peaks (1) and valleys (-1).
Secant (y = sec x): The reciprocal of Cosine (1/cos x). Its “cups” touch the Cosine wave peaks. Because cos(0) = 1, the Secant graph has a vertex at (0,1).
 

 

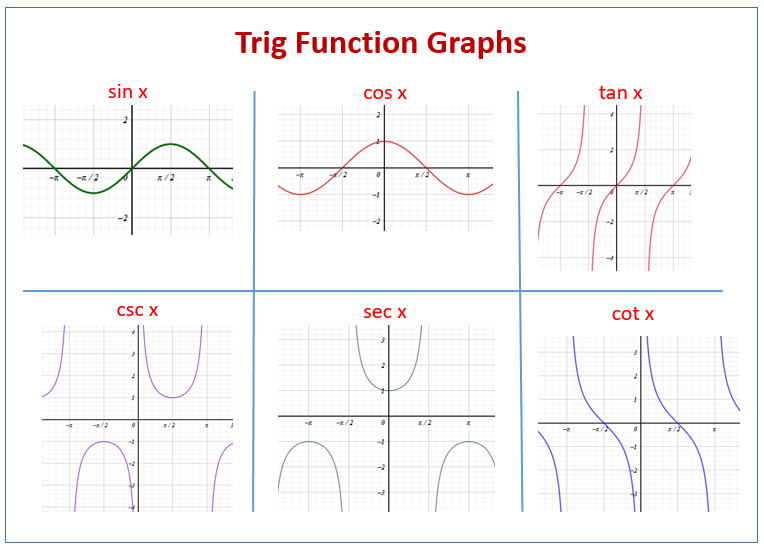
Have a look at this lesson on Trig Function Graphs
Graphing Trig Functions
 

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.