Trigonometric Functions - Sin, Cos, Tan, Csc, Sec and Cot

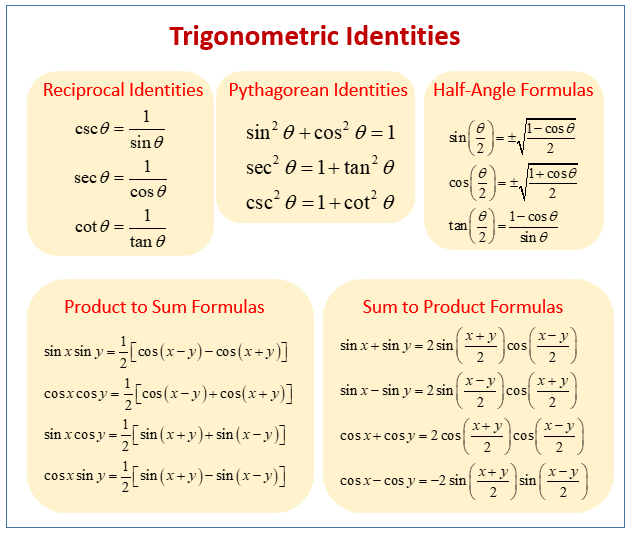
The following diagram shows the trig identities: Reciprocal Identities, Pythagorean Identities, Half-Angle Formulas, Sum and Product Formulas. Scroll down the page for more examples and solutions on the trig identities.

Printable & Online Trigonometry Worksheets

Trigonometric identities are equations involving trigonometric functions that are true for all values of the variables for which both sides of the equation are defined. They’re essential tools in trigonometry, calculus, and many other areas of mathematics and science.

Here are some of the important categories of trigonometric identities:

1. Reciprocal Identities:
   These identities define the reciprocal trigonometric functions in terms of sine, cosine, and tangent:
   csc(θ) = 1/sin(θ)
   sec(θ) = 1/cos(θ)
   cot(θ) = 1/tan(θ)
   

2. Quotient Identities:
   These identities express tangent and cotangent in terms of sine and cosine:
   tan(θ) = sin(θ)/cos(θ)
   cot(θ) = cos(θ)/sin(θ)
   

3. Pythagorean Identities:
   sin²(θ) + cos²(θ) = 1
   1 + tan²(θ) = sec²(θ)
   1 + cot²(θ) = csc²(θ)
   sin²(θ) = 1 - cos²(θ)
   cos²(θ) = 1 - sin²(θ)
   

4. Even-Odd Identities (Parity Identities):
   These identities describe the symmetry of trigonometric functions:
   sin(-θ) = -sin(θ) (sine is an odd function)
   cos(-θ) = cos(θ) (cosine is an even function)
   tan(-θ) = -tan(θ) (tangent is an odd function)
   csc(-θ) = -csc(θ)
   sec(-θ) = sec(θ)
   cot(-θ) = -cot(θ)
   

5. Cofunction Identities:
   These identities relate trigonometric functions of complementary angles:
   sin(π/2 - θ) = cos(θ)
   cos(π/2 - θ) = sin(θ)
   tan(π/2 - θ) = cot(θ)
   cot(π/2 - θ) = tan(θ)
   sec(π/2 - θ) = csc(θ)
   csc(π/2 - θ) = sec(θ)
   

6. Sum and Difference Identities:
   These identities express trigonometric functions of the sum or difference of two angles:
   sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
   sin(α - β) = sin(α)cos(β) - cos(α)sin(β)
   cos(α + β) = cos(α)cos(β) - sin(α)sin(β)
   cos(α - β) = cos(α)cos(β) + sin(α)sin(β)
   tan(α + β) = (tan(α) + tan(β)) / (1 - tan(α)tan(β))
   tan(α - β) = (tan(α) - tan(β)) / (1 + tan(α)tan(β))
   

7. Double-Angle Identities:
   These identities are derived from the sum identities by setting α = β:
   sin(2θ) = 2sin(θ)cos(θ)
   cos(2θ) = cos²(θ) - sin²(θ)
   cos(2θ) = 2cos²(θ) - 1
   cos(2θ) = 1 - 2sin²(θ)
   tan(2θ) = (2tan(θ)) / (1 - tan²(θ))
   

8. Half-Angle Identities:
   These identities express trigonometric functions of half an angle:
   sin(θ/2) = ±√[(1 - cos(θ))/2] (The sign depends on the quadrant of θ/2)
   cos(θ/2) = ±√[(1 + cos(θ))/2] (The sign depends on the quadrant of θ/2)
   tan(θ/2) = sin(θ) / (1 + cos(θ))
   tan(θ/2) = (1 - cos(θ)) / sin(θ)
   

How to define the reciprocal trigonometric functions, the reciprocal identities, and the Pythagorean identities using the unit circle?

• Show Video Lesson

Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities
Use reciprocal, quotient, and Pythagorean identities to determine trigonometric function values.

• Show Video Lesson

Trigonometry Functions - Sin, Cos, Tan, Csc, Sec and Cot

• Show Video Lesson

Tangent, cotangent, secant, and cosecant of any angle

• Show Video Lesson

This tutorial covers the reciprocal identities and shows them in various forms.

• Show Video Lesson

Product To Sum Identities and Sum To Product Formulas
This trigonometry tutorial explains how to simplify trigonometric expressions using the product to sum identities and how to find the exact value of trigonometric expressions using the sum to product formulas.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.