Trigonometric Identities - Simplify Expressions

Trigonometric identities are equalities that involve trigonometric functions and are true for every value of the variables for which both sides of the equality are defined. They are fundamental in simplifying trigonometric expressions, solving trigonometric equations, and proving other identities.

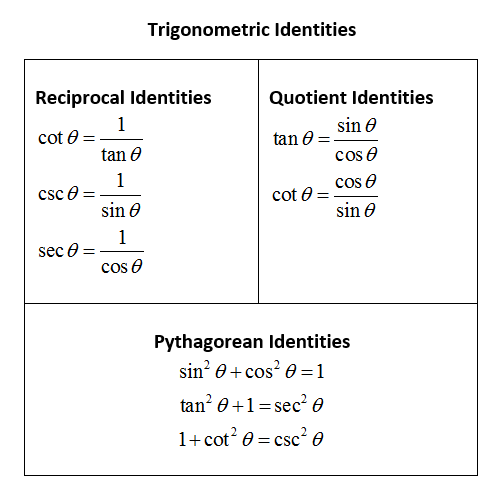
The following are some common Trigonometric Identities: Reciprocal Identities, Quotient Identities and Pythagorean Identities. Scroll down the page for examples and solutions using the identities to simply trigonometric expressions.

 

Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets

More Trig Identities
Check out this other page for more Trig Identities

1. Reciprocal Identities
Sine and Cosecant:
The cosecant (csc) function is the reciprocal of the sine (sin) function.
\(\csc \theta = \frac{1}{\sin \theta}\)
or
\(\sin \theta = \frac{1}{\csc \theta}\)
Cosine and Secant:
The secant (sec) function is the reciprocal of the cosine (cos) function.
\(\cos \theta = \frac{1}{\sec \theta}\)
or
\(\sec \theta = \frac{1}{\cos \theta}\)
Tangent and Cotangent:
The cotangent (cot) function is the reciprocal of the tangent (tan) function
\(\tan \theta = \frac{1}{\cot \theta}\)
or
\(\cot \theta = \frac{1}{\tan \theta}\)

2. Quotient Identities
These identities express the tangent and cotangent functions in terms of sine and cosine functions.
\(\tan \theta = \frac{\sin \theta }{\cos \theta}\)

\(\cot \theta = \frac{\cos \theta}{\sin \theta}\)

3. Pythagorean Identities
Derived from the Pythagorean theorem, these identities relate the squares of the primary trigonometric functions.
\(\sin^2 \theta + \sin^2 \theta = 1\)
\(1 + \tan^2 \theta = \sec^2 \theta\)
\(1 + \cot^2 \theta = \csc^2 \theta\)

Example:
Simplify \(\frac{{\sin \theta \sec \theta }}{{{{\cos }^2}\theta }}\)

Solution:
\(\frac{{\sin \theta \sec \theta }}{{{{\cos }^2}\theta }} = \frac{{\sin \theta \sec \theta }}{{\cos \theta \cos \theta }}\)
\(= \tan \theta \cdot \frac{{\sec \theta }}{{\cos \theta }}\)
= tan θ • sec² θ
= tan θ (tan² θ + 1)
= tan³ θ + tan θ

Example:
Simplify \(\frac{{{{\sin }^2}\theta }}{{\cos \theta }} + \frac{{{{\cos }^2}\theta }}{{\cos \theta }}\)

Solution:
\(\frac{{{{\sin }^2}\theta }}{{\cos \theta }} + \frac{{{{\cos }^2}\theta }}{{\cos \theta }}\)
\(= \frac{{{{\sin }^2}\theta + {{\cos }^2}\theta }}{{\cos \theta }}\)
\(= \frac{1}{{\cos \theta }}\)
= sec θ

Simplifying Trigonometric Expressions Using Identities

Example:
(tan³x)(csc³x)

• Show Video Lesson

How to Simplify Trigonometric Expressions Using Identities?

Example:
sec x cos x − cos² x
(csc² x − 1)(sec² x sin² x)

• Show Video Lesson

Using Identities to Simplify Trigonometric Expressions

Example:
(csc² x − 1)/csc² x
(csc² x − cot² x)/(tan² x - sec² x)

• Show Video Lesson

Algebraic Manipulation of Trigonometric Functions

Distributive Property, FOIL, Factoring.

Example:
cos y(tan y - sec y)
(sin x + cos x)(sin x - cos x)
sin²x cos²x + cos⁴x

• Show Video Lesson

Algebraic Manipulation of Trigonometric Functions with fractions

Simplifying Complex Fractions, Multiplying, Dividing, Adding and Subtracting Fractions.

• Show Video Lesson

Algebraic Manipulation of Trigonometric Functions - Radical Expressions

Multiplying, Dividing, Simplifying. Rationalizing the Denominator.

• Show Video Lesson

Algebraic Manipulation of Trigonometric Functions - Complex Examples

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.