Incenter of a Triangle
Examples, solutions, videos, worksheets, games, and activities to help Geometry students learn how to construct the incenter of a triangle.
What is the Incenter of a Triangle?
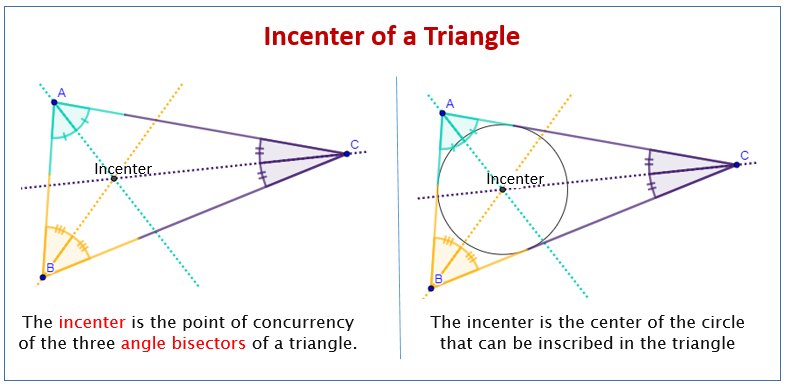
The point of concurrency of the three angle bisectors of a triangle is the incenter. It is the center of the circle that can be inscribed in the triangle, making the incenter equidistant from the three sides of the triangle. The incenter is always located within the triangle.
How to constructing the Incenter?
- Construct two angle bisectors.
- The point where they intersect is the incenter.
The following diagram shows the incenter of a triangle. Scroll down the page for more examples and solutions on the incenters of triangles.
Incenter
This video demonstrates how to construct an incenter and inscribed circle using a compass and straight-edge.
Incenter
Construct the Incenter of a Triangle
Constructing the Incenter
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.