Centroid of a Triangle
Related Topics:
More Lessons for Grade 9
Math Worksheets
Examples, solutions, videos, worksheets, and activities to help Geometry students learn how to construct the centroid of a triangle.
Centroid of a Circle
The centroid of a triangle is one of the four classical triangle centers, along with the orthocenter, circumcenter, and incenter.
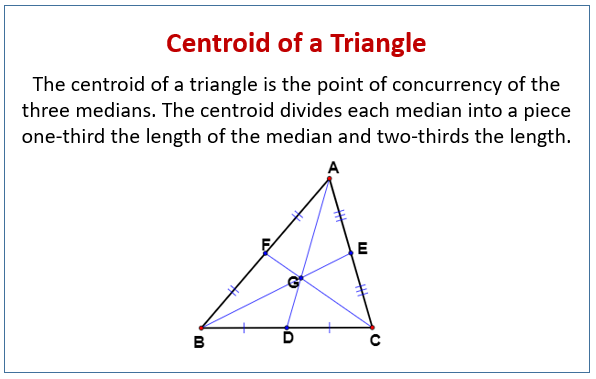
The centroid of a triangle is the point where the three medians of the triangle intersect.
The following diagram shows the centroid of a triangle. Scroll down the page for more examples and solutions on the centroid of a triangle.
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets`
What is a Median?
A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the opposite side.
Every triangle has three medians, one from each vertex.
Each median bisects the side it connects to, dividing that side into two equal parts.
How to Find the Centroid?
To locate the centroid of a triangle:
- Find the midpoint of each side of the triangle.
- Draw a line segment (median) from each vertex to the midpoint of its opposite side.
- The point where these three medians intersect is the centroid.
Key Properties of the Centroid:
- Balances the Triangle – Acts as the “center of mass” (if the triangle were a uniform sheet, it would balance perfectly on the centroid).
- Divides Medians in 2:1 Ratio – The distance from a vertex to the centroid is twice the distance from the centroid to the midpoint of the opposite side.
- Always Inside the Triangle – Unlike the orthocenter or circumcenter, the centroid is always inside the triangle, even for obtuse triangles.
- Equal Area Division: Each median divides the triangle into two smaller triangles of equal area. Furthermore, the three medians divide the triangle into six smaller triangles, all of which have equal areas.
Constructing the Centroid
The centroid is the point of concurrency of the three medians in a triangle. It is the center of mass (center of gravity) and therefore is always located within the triangle. The centroid divides each median into a piece one-third the length of the median and two-thirds the length. To find the centroid, we find the midpoint of two sides in the coordinate plane and use the corresponding vertices to get equations.
Construction of a Triangle Centroid
The Centroid
The point of concurrency of the three medians is the Centroid.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.