Triangles

Related Topics:
GRE Math
Math Worksheets



This lesson is part of a series of lessons for the quantitative reasoning sectionof the GRE revised General Test. In this lesson, we will learn:

• angles and sides of triangles
• types of triangles
• Pythagorean Theorem
• special right triangles
• area of a triangle
• congruent triangles
• similar triangles

Triangles

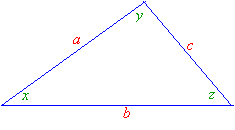
Every triangle has three sides and three interior angles. The measures of the interior angles add up to 180°.

The length of each side must be less than the sum of the lengths of the other two sides. For example, the sides of a triangle could not have the lengths 4, 7, and 12 because 12 is greater than 4 + 7.

We can also say that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.

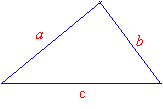
For the above triangle:

a + b > c
b + c > a
a + c > b

 

Types of Triangles

The following are some types of triangles.

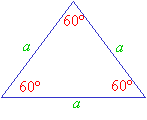
• A triangle with three congruent sides is called an equilateral triangle. The measures of the three interior angles of such a triangle are also equal, and each measure is 60°.

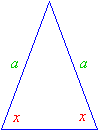
• A triangle with at least two congruent sides is called an isosceles triangle. If a triangle has two congruent sides, then the angles opposite the two sides are congruent. The converse is also true i.e. if the angles opposite the two sides are congruent then the sides are congruent.

• A triangle with an interior right angle is called a right triangle. The side opposite the right angle is called the hypotenuse; the other two sides are called legs.

Pythagorean Theorem

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.

If we take the length of the hypotenuse to be c and the length of the legs to be a and b then this theorem tells us that:

c² = a² + b²

The Pythagorean Theorem can be used when we know the length of two sides of a right triangle and we need to get the length of the third side.

Example: Find the length of one side of a right triangle if the length of the hypotenuse is 10 inches and the length of the other side is 9 inches.

Solution:
Step 1: Write down the formula	c2 = a2 + b2
Step 2: Plug in the values	102 = 92 + b2
	100 = 81 + b2
Step 3: Subtract 81 from both sides	19 = b2
	b =
	b » 4.36

Answer: The length of the side is 4.36 inches.

Special Right Triangles

The Pythagorean theorem can be used to determine the ratios of the sides of two special right triangles.

One special right triangle is an isosceles right triangle which has two congruent sides and angles 45°- 45°- 90°.

Applying the Pythagorean theorem to such a triangle shows that the lengths of its sides are in the ratio of .

 

The other special right triangle is a 30°- 60°- 90° right triangle, which is half of an equilateral triangle, as indicated below. The lengths of the sides of a 30°- 60°- 90° triangle are in the ratio of .

            

Area of a Triangle

The area of a triangle equals one-half the product of the length of a base and the height corresponding to the base.

Area =

In the figure below, the base is denoted by b and the corresponding height is denoted by h. The height of a triangle is the perpendicular distance from a vertex to the base of the triangle.

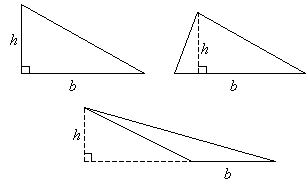
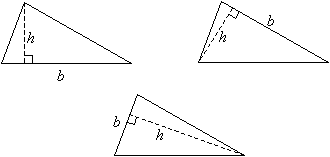
Any side of a triangle can be used as a base; the height that corresponds to the base is the perpendicular line segment from the opposite vertex to the base (or to an extension of the base).

Congruent Triangles

Two triangles that have the same shape and size are called congruent triangles. More precisely, two triangles are congruent if their vertices can be matched up so that the corresponding angles and the corresponding sides are congruent.

The following three propositions can be used to determine whether two triangles are congruent by comparing only some of their sides and angles.
• If the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent.
• If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
• If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.

Similar Triangles

Two triangles that have the same shape but not necessarily the same size are called similar triangles. More precisely, two triangles are similar if their vertices can be matched up so that the corresponding angles are congruent or, equivalently, the lengths of corresponding sides have the same ratio, called the scale factor of similarity.

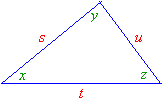
When we say that triangles ABC and DEF are similar, it is assumed that angles A and D are congruent, angles B and E are congruent, and angles C and F are congruent, as shown in the figure below. In other words, the order of the letters indicates the correspondences.

If the above two triangles are similar then

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.