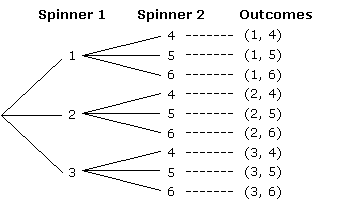
Tree Diagrams
Related Pages
Using Tree Diagrams In Probability
Probability Tree Diagrams
More Lessons On Probability
Probability Worksheets
In these lessons, we will look at more examples of probability word problems.
We will use tree diagrams to help us solve the problems.
We will see that tree diagrams can be used to represent the set of all possible outcomes
involving one or more experiments.
Tree diagrams are visual tools used in probability to visualize and calculate the likelihood of different outcomes in a sequence of events. They are particularly helpful when dealing with multiple events occurring one after another, either independently or dependently.
Probability tree diagrams are useful for both independent (or unconditional) probability and dependent (or conditional) probability.
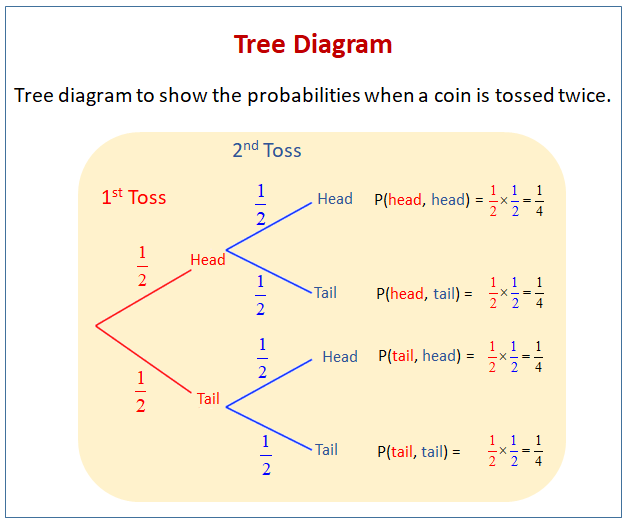
The following tree diagram shows the probabilities when a coin is tossed two times. Scroll down the page for more examples and solutions on using probability tree diagrams.
Probability Worksheets
Practice your skills with the following probability worksheets:
Printable & Online Probability Worksheets
Key Rules for Probability Trees
- Multiply probabilities along branches for combined events.
- Add probabilities for different paths leading to the same outcome.
- Check probabilities sum to 1 at each stage.
Tree Diagrams For Independent Events
Example:
Julia spins 2 spinners; one of which is labeled 1, 2 and 3, and the other is labeled 4, 5
and 6.
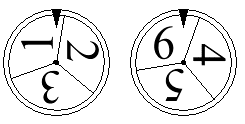
a) Draw a tree diagram for the experiment.
b) What is the probability that the spinners stop at “3” and “4”?
c) Find the probability that the spinners do not stop at “3” and
“4”.
d) What is the probability that the first spinner does not stop at “1”?
-
Show Solution
a) Tree diagram for the experiment.

b) The probability that the spinners stop at “3” and “4”
n(S ) = 9
Probability that the spinners stop at (3,4) =
c) The probability that the spinners do not stop at “3” and “4”
Probability that the spinners do not stop at (3,4) =
d) The probability that the first spinner does not stop at “1”
Probability that the first spinner stop at “1” =
Probability that the first spinner does not stop at “1” =
Example:
Box A contains 3 cards numbered 1, 2 and 3. Box B contains 2 cards numbered 1 and 2. One card
is removed at random from each box.
a) Draw a tree diagram to list all the possible outcomes.
b) Find the probability that:
(i) the sum of the numbers is 4
(ii) the sum of the two numbers is even.
(iii) the product of the two numbers is at least 5.
(iv) the sum is equal to the product.
-
Show Solution
a) A tree diagram of all possible outcomes.

b) The probability that:
(i) the sum of the numbers is 4.
Let S be the sample space and A be the event that the sum is 4.
n(S) = 6; n(A) = 2
P(A) =
(ii) the sum of the two numbers is even.
Let B be the event that the sum is even.
n(B) = 3
P(B) =
(iii) the product of the two numbers is at least 5.
Let C be the event that the product of the two numbers is at least 5.
n(C) = 1
P(C) =
(iv) the sum is equal to the product.
Let D be the event that the sum of the two numbers is equal to the product.
n(D) = 1
P(D) =
Example:
A bag contains 4 cards numbered 2, 4, 6, 9. A second bag contains 3 cards numbered 2, 3, 6.
One card is drawn at random from each bag.
a) Draw a tree diagram for the experiment.
b) With the help of the tree diagram, calculate the probability that the two numbers obtained:
(i) have different values.
(ii) are both even.
(iii) are both prime.
(iv) have a sum greater than 5.
(v) have a product greater than 16.
-
Show Solution
Solution:
a) A tree diagram of all possible outcomes.

b) The probability that the two numbers obtained:
(i) have different values.
Let S be the sample space and A be the event that the two values are different
n(S) = 12 ; n(A) = 10
P(A) =
(ii) are both even.
Let B be the event that both values are even.
n(B) = 6
P(B) =
(iii) are both prime.
Let C be the event that both values are prime.
n(C) = 2
P(C) =
(iv) have a sum greater than 5.
Let D be the event that the sum of both values is greater than 5.
n(D) = 10
P(D) =
(v) have a product greater than 16.
Let E be the event that the product of both values is greater than 16.
n(E) = 6
P(E) =
How to use probability tree diagrams for independent events (or unconditional probability)?
Example:
Jenny has a bag with 7 blue sweets and 3 red sweets. She picks a sweet at random from the bag,
replaces it and picks again at random. Draw a tree diagram to represent this situation and
use it to calculate the probabilities that she picks
a) 2 red sweets
b) no red sweets
c) at least 1 blue sweet
d) 1 sweet of each color
How to do a probability tree?
Probability Trees and Independent Events
Multiplying and adding probabilities of independent events
Example:
Sarah picks a marble from a bag. There are 8 marbles in the bag and 5 of them are green.
The rest are red. She looks at the marble and then places it into the bag. She then picks
another marble. Complete a probability tree.
How to solve probability problems using tree diagrams?
The following videos gives more examples of solving probability problems using tree diagrams. A tree diagram can help you generate all the outcomes.
Example:
Show the possible outcomes of playing Rock, Paper, Scissors. Find the probability of a
tie game.
Example:
You are ordering a sandwich. Make a list of all the possibilities.
Bread - white, sourdough
Meat - ham, turkey
Cheese - American, Provolone
Find the probability of making a sandwich with both white bread and ham.
Tree Diagrams For Dependent Events
Example:
Jimmy has a bag with seven blue sweets and 3 red sweets in it.
He picks up a sweet at random from the bag, but does not replaces it and then picks again at random.
Draw a tree diagram to represent this situation and use it to calculate the probabilities that he picks:
(a) two red sweets
(b) no red sweets
(c) at least one blue sweet
(d) one sweet of each color
Probability Diagrams for events that involve with and without replacements.
Example:
A bag contains 4 red sweets and 5 blue sweets. Draw a probability tree diagram when
a) the sweets are taken with replacement.
b) the sweets are taken without replacement.
Example:
A bag contains four light bulbs, of which two are defective.
We draw bulbs without replacement until a working bulb is selected.
Set up the tree diagram for this experiment, find the probability of each outcome, and determine the probability that at most two draws occur.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.