Set Theory: Subsets

Sets & Set Notations
Subsets & Proper Subsets	Number of Subsets Formula	Subset Video Lessons

Subsets & Proper Subsets

If every member of set A is also a member of set B, then A is a subset of B, we write A ⊆ B. We can say A is contained in B.

We can also say B ⊇ A, B is a superset of A, B includes A, or B contains A.

If A is not a subset of B, we write A ⊈ B.

If A is a subset of B (A ⊆ B), but A is not equal to B, then we say A is a proper subset of B, written as A ⊂ B or A ⊊ B.

The following diagram shows an example of subset. Scroll down the page for more examples and solutions on subsets.

 

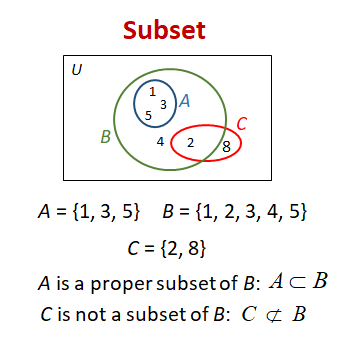
Example:
A = {1, 3, 5}, B = {1, 2, 3, 4, 5}, C = {1, 2, 3, 4, 5}
A is a subset of B, A ⊆ B. because every element in A is also in B
A is also proper subset of B, A ⊂ B. because every element in A is also in B and A ≠ B
C is subset of B, C ⊆ B. but is not a proper subset of B because C = B

Example:

X = {1, 3, 5}, Y = {2, 3, 4, 5, 6}.
X is not a subset of Y, X ⊈ Y, because the element 1 is in X but not in Y.

Note:

• The empty set denoted by ∅ or {} is a subset of any set.
  ∅ ⊆ S
• The empty set is a proper subset of all sets except ∅
  ∅ ⊂ S ≠ ∅

Example:
List all the subsets and proper subsets of the set Q = {x, y, z}

Solution:
The subsets of Q are { }, {x}, {y}, {z}, {x, y}, {x, z}, {y, z} and {x, y, z}
The proper subsets of Q are { }, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}

What Is The Formula For The Number Of Subsets And Proper Subsets?

The number of subsets for a finite set A is given by the formula:
If set A has n elements, it has 2ⁿ subsets.
If set A has n elements, it has 2ⁿ - 1 proper sets.

Example:
Q = {x, y, z}. How many subsets and proper subsets will Q have?

Solution:
Q has 3 elements
Number of subsets = 2³ = 8
Number of proper subsets = 7

Example:
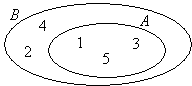
Draw a Venn diagram to represent the relationship between the sets. A = {1, 3, 5} and B = {1, 2, 3, 4, 5}

Solution:
Since A is a subset of B:
Step 1: Draw circle A within the circle B

Step 2: Write down the elements in circle A.

Step 3: Write down the remaining elements in circle B

 

Sets Worksheets

Subset Worksheets
Distinguish between subsets and proper subsets. Find the number of subsets in a given set.

Sets Worksheets
More Worksheets for Sets

Subset And Proper Subset

This video defines and give the notation or symbols used for subsets and proper subsets and shows how to determine the number of possible subsets for a given set.

• Show Video Lesson

Finding the Number of Subsets of a Set

How do we find the number of subsets a set has? How many subsets does any given set has? In this video we go over some example problems, calculating the number of subsets a set has.
If a set has n elements then it has 2ⁿ subsets.

• Show Video Lesson

• Solutions to the Practice Problems in the video
  1. The empty set has 0 elements, so it has 2⁰ = 1 subsets. The only subset of the empty set is the empty set itself.
  2. This set has 6 elements. They are the numbers 3, 4, and 7, the set { 3, 4, 7 }, and the numbers 34 and 73. Thus, it has 2⁶ = 64 subsets.
  3. This set has 8 elements. They are the numbers 4, 2³, 0, and 2, the interval [1, 2], the sets { 1, 9, 10 } and { }, and the 3-tuple (2, 3, 4). Thus, it has 2³ = 256 elements.

How To Distinguish Between Elements, Subsets And Proper Subsets?

Example:
Indicate whether true or false:
{} ⊆ {2, 3}
{} ∈ {2, 3}
{} ∈ {{}, 2, 3}
{5, 6, 7} ⊆ {5, 6, 7, 8}
{5, 6, 7, 8} ⊆ {5, 6, 7, 8}
{5, 6, 7, 8} ⊂ {5, 6, 7, 8}

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.