Pythagorean Triples

Pythagorean Triples

A Pythagorean triple consists of three positive integers a,b, and c, such that a² + b² = c². This relationship is derived directly from the Pythagorean theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides (legs).

We may write the triple as (a, b, c).

For example, the numbers 3, 4 and 5 form a Pythagorean Triple because 3² + 4² = 5². There are infinitely many Pythagorean triples.

Some examples are:

( 3 , 4 , 5 )	( 5, 12, 13)	( 7, 24, 25)	( 8, 15, 17)
( 9, 40, 41)	(11, 60, 61)	(12, 35, 37)	(13, 84, 85)
(16, 63, 65)	(20, 21, 29)	(28, 45, 53)	(33, 56, 65)
(36, 77, 85)	(39, 80, 89)	(48, 55, 73)	(65, 72, 97)

Families of Pythagorean Triples

If we multiply each number of a Pythagorean triple by the same number, we form another Pythagorean triple.

For example, (6, 8, 10) is a family of the Pythagorean triple (3, 4, 5) because it can be obtained by 2 × 3 = 6, 2 × 4 = 8, 2 × 5 = 10. If we multiply (3, 4, 5) by 3, we get another triple (9, 12, 15). This can be repeated with different multiples.

Similarly, the family for (5, 12, 13) would be (10, 24, 26), (15, 36, 39) and so on.

Pythagorean Triples and Right Triangles

When we make a triangle with sides whose lengths are the Pythagorean Triples, the triangle will form a right triangle. This follows from the converse of the Pythagorean Theorem.

The following diagram shows some examples of Pythagorean Triples. Scroll down the page for more examples and solutions on Pythagorean Triples and Right Triangles.

• Printable & Online Pythagorean Theorem Worksheets

  Printable
  Pythagorean Theorem Find the length of the hypotenuse or side, check for right triangle, Pythagorean Theorem word problems
  

  Online
  Pythagorean Theorem
  Find the missing side
  Test for right triangle
  Pythagorean Theorem Word Problems
  Converse Pythagorean Theorem, Types of Triangles

Memorizing some common Pythagorean triples can helpful.

For example, if we see that the sides of a triangle form a Pythagorean triple then we know that it is a right triangle.

The following video gives some examples of Pythagorean triples and right triangles.
Any group of 3 integer values that satisfies the equation a² + b² = c² is called a Pythagorean Triple. Therefore, any triangle that has sides that form a Pythagorean Triple must be a right triangle.

• Show Video Lesson

Solving Problems Using The Pythagorean Triples

Pythagorean triples may also help us to find the missing side of a right triangle faster. If two sides of a right triangle form part of a triple then we can know the value of the third side without having to calculate using the Pythagorean theorem.

Example:
Find the value of x

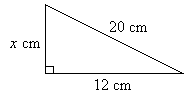
Solution:
Check for Pythagorean triple:
Get the ratio of the two given sides:
12 : 20 = 3 : 5 ( divide by 4 )

From the ratio, we know that it is a Pythagorean triple.
So, x = 4 × 4 = 16 cm

The following videos show how to solve some GMAT, SAT and ACT questions using the Pythagorean Triples

• Show Video Lesson

How To Generate Pythagorean Triples

The following video will show you how to use an ordinary multiplication table to list infinitely many different examples of Pythagorean Triples.

• Show Video Lesson

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.