Simplifying Rational Expressions

What Is A Rational Expression?

A rational expression is a fraction in which the numerator and/or the denominator are polynomials.

Examples:

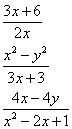
The following diagram shows how to simplify rational expressions. Scroll down the page for more examples and solutions on simplifying rational expressions.

Printable & Online Algebra Worksheets

How To Simplify Rational Expressions?

In this lesson, we will look at simplifying rational expressions. A rational expression has been simplified or reduced to lowest terms if all common factors from the numerator and denominator have been canceled.

1. We first need to factor the polynomials
2. Cancel any common factors from the top and bottom of the rational expression.

Example:
Simplify each of the following rational expressions:

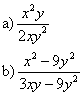
Solution:

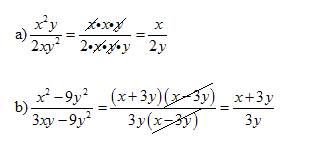
Simplifying Rational Expressions - Level 1

Example:
Simplify
(4x³ + 8x²)/2x

• Show Video Lesson

Simplifying Rational Expressions - Level 2

Example:
Simplify
(7x² + 28x)/(x² + 8x + 16)

• Show Video Lesson

Simplifying Rational Expressions - Level 3

Example:
Simplify
(4x² + 4x + 1)/(2x³ + 11x² + 5x)

• Show Video Lesson

How To Write Rational Expressions In Lowest Terms?

Step 1: Factor them
Step 2: Cancel to write in lowest terms
Give the domain of the expressions

Examples:
Simplify
a) (x + 2)/(x² + 5x + 6)
b) (x² + 2x - 15)/(x² + x - 12)

• Show Video Lesson

Rational Expressions: Writing In Lowest Terms

How to reduce a rational expression involving a cubic polynomial and a quadratic polynomial?

Example:
Simplify
(x³ + 1)/(x² + 7x + 6)

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.