

Scalar Multiplication of Vectors
Related Topics:
Common Core (Vector and Matrix Quantities)
Common Core for Mathematics
Examples, solutions, videos, and lessons to help High School students learn how to represent scalar multiplication graphically by scaling vectors and possibly reversing their direction; perform scalar multiplication component-wise, e.g., as c(vx, vy) = (cvx, cvy).
The following diagram shows how to multiply a vector by a scalar. Scroll down the page for more examples and solutions of scalar multiplication.
This video shows how to multiply a vector by a scalar including some algebraic properties of scalar multiplication. The lesson also discusses briefly the concept of a linear combination of vectors and shows an example of drawing a geometric sum/difference of 3 vectors.
Vector Addition and Scalar Multiplication, Example 1
In this video, we look at vector addition and scalar multiplication algebraically using the component form of the vector.
Vector Addition and Scalar Multiplication, Example 2
In this video we add two vectors in component form and also sketch the vectors to illustrate how to add vectors graphically. Vectors, Addition, Subtraction and Scalar Multiplication Multiplying a Vector by a Scalar
This lesson presents the properties of multiplication of a vector by a scalar. You will also learn what collinear vectors represent and how to verify that two vectors are collinear or parallel.



Common Core (Vector and Matrix Quantities)
Common Core for Mathematics
Examples, solutions, videos, and lessons to help High School students learn how to represent scalar multiplication graphically by scaling vectors and possibly reversing their direction; perform scalar multiplication component-wise, e.g., as c(vx, vy) = (cvx, cvy).
Suggested Learning Targets
- I can multiply a vector by a scalar graphically.
- I can multiply a vector by a scalar component-wise.
The following diagram shows how to multiply a vector by a scalar. Scroll down the page for more examples and solutions of scalar multiplication.
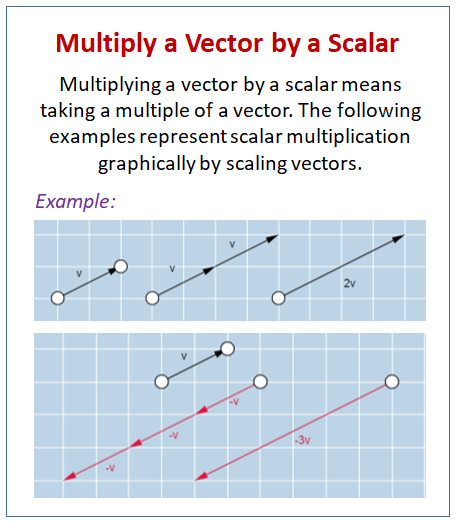
This video shows how to multiply a vector by a scalar including some algebraic properties of scalar multiplication. The lesson also discusses briefly the concept of a linear combination of vectors and shows an example of drawing a geometric sum/difference of 3 vectors.
In this video, we look at vector addition and scalar multiplication algebraically using the component form of the vector.
In this video we add two vectors in component form and also sketch the vectors to illustrate how to add vectors graphically. Vectors, Addition, Subtraction and Scalar Multiplication Multiplying a Vector by a Scalar
This lesson presents the properties of multiplication of a vector by a scalar. You will also learn what collinear vectors represent and how to verify that two vectors are collinear or parallel.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.