Properties of Rhombus
Related Pages
Quadrilaterals
Angles In A Quadrilateral
Polygons
More Geometry Lessons
Math Worksheets
These lessons, with videos, examples and step-by-step solutions, help Geometry students learn about the properties of a rhombus.
A rhombus is a type of quadrilateral (4-sided polygon) with unique characteristics.
The following diagram shows the properties of a rhombus. Scroll down the page for more examples and solutions on using the properties of a rhombus.
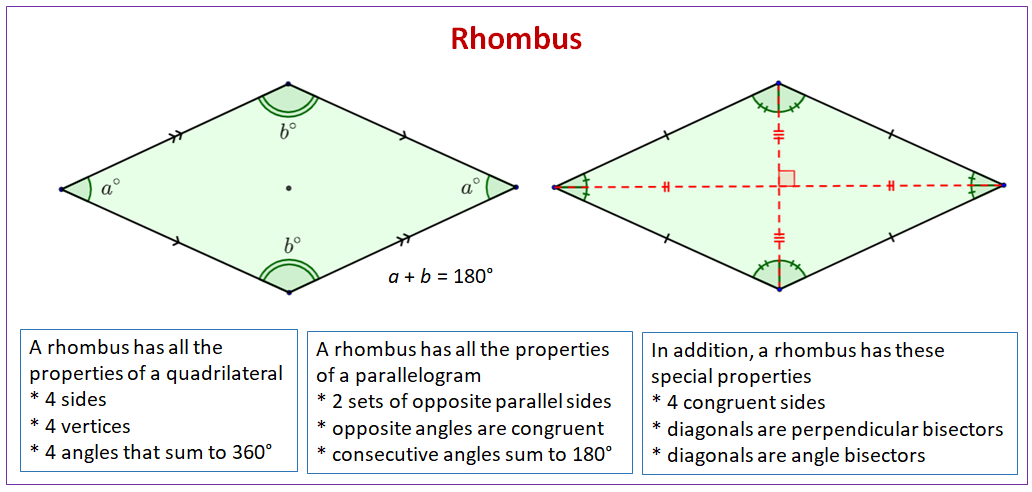
What are the Properties of a Rhombus?
A rhombus is a quadrilateral and has all the properties of a quadrilateral
- 4 sides
- 4 vertices
- 4 angles that sum to 360°
A rhombus is a parallelogram and has all the properties of a parallelogram
- 2 sets of opposite parallel sides
- opposite angles are congruent
- consecutive angles sum to 180°
In addition, a rhombus has these special properties
- 4 congruent sides
- diagonals are perpendicular bisectors
- diagonals are angle bisectors
A square is a rhombus with all its angles equal to 90°. Therefore, every square is a rhombus, but not every rhombus is a square.
Symmetry:
- A rhombus has two lines of symmetry, which are its diagonals.
- It has rotational symmetry of order 2 (180°). This means it looks the same after being rotated 180° about the intersection of its diagonals.
Perimeter
The formula for the perimeter of a rhombus is
\( P = 4 \times side \)
Area
The formula for the area of a rhombus is
\(A = base \times height \)
or
\(A = \frac{d_1 \times d_2 }{2} \) (diagonals)
Apply the properties of a rhombus to solve problems
Rhombus Properties
Properties of rhombi often show up in geometric proofs and many other types of problems.
All parallelogram properties apply to rhombus properties since a rhombus is a type of parallelogram.
In a rhombus, there are
- two pairs of parallel sides,
- four sides that are all congruent to each other,
- diagonals that bisect the angles, and
- diagonals that are perpendicular bisectors of each other.
Properties of a Rhombus
A rhombus is a quadrilateral with congruent sides and opposite angles that are congruent.
This video will cover the number of sides of a rhombus, the angles of a rhombus.
In addition, it cover how to find the area of a rhombus and the perimeter.
Properties of a Rhombus
The diagonals of a rhombus are perpendicular and bisect the angles of the rhombus
Area of a Rhombus - Geometry Help
Students learn the formula for the area of a rhombus, and are asked to solve problems using this formula.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.