Probability and Area
In these lessons, we will learn how to solve a variety of probability involving areas.
Related Pages
Probability Problems
Probability Tree Diagrams
Probability Without Replacement
Theoretical vs. Experimental Probability
More Lessons On Probability
Probability can also relate to the areas of geometric shapes. The following are some examples of probability problems that involve areas of geometric shapes.
Probability Of Shaded Region
Example:
A dart is thrown at random onto a board that has the shape of a circle as shown below. Calculate the
probability that the dart will hit the shaded region. (Use π = 3.142)
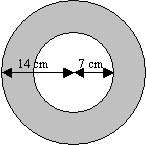
Solution:
Total area of board = 3.142 × 14 2 = 615.83 cm2
Area of non-shaded circle = 3.142 × 7 2 = 153.99 cm2
Area of shaded region = 615.83 – 153.99 = 461.84 cm2 = 462 cm2 (rounded to whole number)
Probability of hitting the shaded region = 
Example:
The figure shows a circle divided into sectors of different colors.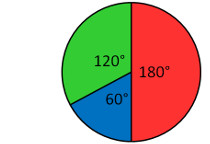 
If a point is selected at random in the circle, calculate the probability that it lies:
a) in the red sector
b) in the green sector.
c) in any sector except the green sector.
Solution:
Total area of board = 3.142 × 14 2 = 615.83 cm2
a) Area of red sector = 
× area of circle
Probability that the point lies on red sector =
b) Area of green sector = 
× area of circle
Probability that the point lies on green sector =
c) in any sector except the green sector.
Probability that the point does not lie in the green sector = 
Example:
In the figure below, PQRS is a rectangle, and A, B, C, D are the midpoints of the respective sides as shown.
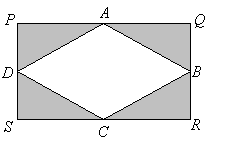
An arrow is shot at random onto the rectangle PQRS. Calculate the probability that the arrow strikes:
a) triangle AQB.
b) a shaded region.
c) either triangle BRC or the unshaded region.
Solution:
a) Let PQ = 2x and QR = 2y. Then, AQ = x and QB = y.
Area of rectangle PQRS = 2x × 2y = 4xy
Area AQB = xy
Probability of striking triangle AQB = xy ÷ 4xy = 
b) All the shaded triangles are equal.
Total area of shaded regions = 4 × xy = 2xy
Probability of striking a shaded region = 2xy ÷ 4xy =
c) Area of unshaded region = 4xy – 2xy = 2xy
Probability of striking unshaded region = 2xy ÷ 4xy =
Area of triangle BRC = xy
Probability of striking triangle BRC = 
Probability of striking triangle BRC or unshaded region = 
Geometric Probability using Area
Example 1: A circle with radius 2 lies within a square with side length 6. A dart lands randomly inside the square. What is the probability that the dart lands inside the circle? Give the exact probability and the probability as a percent rounded to the nearest tenths.
Example 2: A point is chosen at random on this figure. What is the probability that the point is in the yellow region?
Example 3: A square is inscribed inside a circle. What is the probability that a point chosen at random inside the circle will be inside the square?
Example 4: A circle is inscribed in an equilateral triangle. What is the probability that a point chosen at random in the triangle will be inside the circle?
Problem 1: Find the probability that a point chosen at random inside the circle will be inside the shaded region.
Problem 2: Find the probability that a point chosen at random inside the square will be inside the shaded region.
Area Probability Problem: Rectangle within a rectangle
Example: Find the probability that a point randomly selected from a figure would land in the shaded area.
Area Probability Problem 2
Area Probability Problem 3
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.