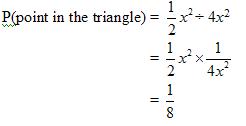Probability Word Problems

Here we will be looking into solving probability word problems involving:

• Probability and Sample Space
• Probability and Frequency Table
• Probability and Area
• Probability of Simple Events
• Probability and Permutations
• Probability and Combinations
• Probability of Independent Events

The following diagram gives the types of probability, formulas and examples. Scroll down the page for more examples and solutions on how to solve probability problems.

Probability Worksheets
Practice your skills with the following worksheets:
Printable & Online Probability Worksheets

We will now look at some examples of probability problems.

Example:
At a car park there are 100 vehicles, 60 of which are cars, 30 are vans and the remainder are lorries. If every vehicle is equally likely to leave, find the probability of:
a) a van leaving first.
b) a lorry leaving first.
c) a car leaving second if either a lorry or van had left first.

Types of Probability Problems and Examples
1. Simple Probability
This involves calculating the probability of a single event.
Problem: What is the probability of rolling an even number on a standard six-sided die?
P(even number)=\(\frac{3}{6}=\frac{1}{2}\)

2. Independent Events (And)
Two events are independent if the outcome of one does not affect the outcome of the other.
Rule: P(A and B)=P(A)×P(B)
Problem: What is the probability of flipping a coin and getting heads, and then rolling a standard six-sided die and getting a 4?
P(Heads and 4)=P(Heads)×P(4) = \(\frac{1}{2}×\frac{1}{6}=\frac{1}{12}\).

3. Dependent Events (And, Without Replacement)
Two events are dependent if the outcome of the first event does affect the outcome of the second event.
Rule: P(A and B)=P(A)×P(B|A) (where P(B|A) is the probability of B given A has occurred).
Problem: You have a bag with 5 red marbles and 5 blue marbles. What is the probability of drawing a red marble, then (without replacing the first) drawing a blue marble?
After Event A, there are now 5 blue marbles left and 9 total marbles.
Drawing a blue marble given the first was red. P(B|A)=\(\frac{5}{9}\).
P(Red and Red)=P(A)×P(B|A)=\(\frac{5}{10}×\frac{5}{9}=\frac{5}{18}\).

4. Mutually Exclusive Events (Or)
Two events are mutually exclusive if they cannot happen at the same time (they have no outcomes in common).
Rule: P(A or B)=P(A)+P(B)
Problem: What is the probability of rolling a 2 OR a 5 on a standard six-sided die?
P(2 or 5)=P(A)+P(B)=\(\frac{1}{6}+\frac{1}{6}=\frac{2}{6}=\frac{1}{3}\)

5. Non-Mutually Exclusive Events (Or)
Two events are non-mutually exclusive if they can happen at the same time (they share one or more outcomes).
Rule: P(A or B)=P(A)+P(B)−P(A and B).
Problem: What is the probability of rolling an even number OR a number greater than 3?
They are non-mutually exclusive because you can roll a number that is both even and greater than 3 (specifically, 4 and 6).
P(even and number greater than 3)=\(\frac{2}{6} = \frac{1}{3}\).
P(even or number greater than 3)=P(A)+P(B)−P(A and B)=\(\frac{1}{2}+\frac{1}{2}-\frac{1}{3}=\frac{2}{3}\)

Solution:
a) Let S be the sample space and A be the event of a van leaving first.
n(S) = 100
n(A) = 30

Probability of a van leaving first:

b) Let B be the event of a lorry leaving first.
n(B) = 100 – 60 – 30 = 10
Probability of a lorry leaving first:

c) If either a lorry or van had left first, then there would be 99 vehicles remaining, 60 of which are cars. Let T be the sample space and C be the event of a car leaving.
n(T) = 99
n(C) = 60

Probability of a car leaving after a lorry or van has left:

Example:
A survey was taken on 30 classes at a school to find the total number of left-handed students in each class. The table below shows the results:

No. of left-handed students	0	1	2	3	4	5
Frequency (no. of classes)	1	2	5	12	8	2

A class was selected at random.
a) Find the probability that the class has 2 left-handed students.
b) What is the probability that the class has at least 3 left-handed students?
c) Given that the total number of students in the 30 classes is 960, find the probability that a student randomly chosen from these 30 classes is left-handed.

• Show Solution

  a) Let S be the sample space and A be the event of a class having 2 left-handed students.
  n(S) = 30
  n(A) = 5

  
  
  

  b) Let B be the event of a class having at least 3 left-handed students.
  n(B) = 12 + 8 + 2 = 22

  
  
  

  c) First find the total number of left-handed students:
  

  No. of left-handed students, x	0	1	2	3	4	5
  Frequency, f (no. of classes)	1	2	5	12	8	2
  fx	0	2	10	36	32	10

  
  

  Total no. of left-handed students = 2 + 10 + 36 + 32 + 10 = 90

  Here, the sample space is the total number of students in the 30 classes, which was given as 960.

  Let T be the sample space and C be the event that a student is left-handed.
  n(T) = 960
  n(C) = 90

  

Probability And Area

Example:
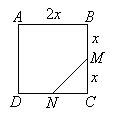
ABCD is a square. M is the midpoint of BC and N is the midpoint of CD. A point is selected at random in the square. Calculate the probability that it lies in the triangle MCN.

 

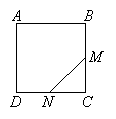
• Show Solution

  Let 2x be the length of the square.
  
  

  Area of square = 2x × 2x = 4x²

  Area of triangle MCN is
  

  

This video shows some examples of probability based on area.

• Show Video Lesson

Probability Of Simple Events

The following video shows some examples of probability problems. A few examples of calculating the probability of simple events.

Example:

1. What is the probability of the next person you meeting having a phone number that ends in 5?
2. What is the probability of getting all heads if you flip 3 coins?
3. What is the probability that the person you meet next has a birthday in February? (Non-leap year)

• Show Video Lesson

This video introduces probability and gives many examples to determine the probability of basic events.

Example:

1. A bag contains 8 marbles numbered 1 to 8
   a. What is the probability of selecting a 2 from the bag?
   b. What is the probability of selecting an odd number?
   c. What is the probability of selecting a number greater than 6?
   

2. Using a standard deck of cards, determine each probability.
   a. P(face card)
   b. P(5)
   c. P(non face card)

• Show Video Lesson

Using Permutations To Solve Probability Problems

This video shows how to evaluate factorials, how to use permutations to solve probability problems, and how to determine the number of permutations with indistinguishable items.

A permutation is an arrangement or ordering. For a permutation, the order matters.

Examples:

1. If a class has 28 students, how many different arrangements can 5 students give a presentation to the class?
2. How many ways can the letters of the word PHEONIX be arranged?
3. How many ways can you order 3 blue marbles, 4 red marbles and 5 green marbles? Marbles of the same color look identical.

• Show Video Lesson

Using Combinations To Solve Probability Problems

This video shows how to evaluate combinations and how to use combinations to solve probability problems.

A combination is a grouping or subset of items. For a combination, the order does not matter.

Examples:

1. The soccer team has 20 players. There are always 11 players on the field. How many different groups of players can be in the field at the same time?
2. A student needs 8 more classes to complete her degree. If she has met the prerequisites for all the courses, how many ways can she take 4 class next semester?
3. There are 4 men and 5 women in a small office. The customer wants a site visit from a group of 2 men and 2 women. How many different groups van be formed from the office?

• Show Video Lesson

How To Find The Probability Of Different Events?

This video explains how to determine the probability of different events. This can be found that can be found using combinations and basic probability.

1. The probability of drawing 2 cards that are both face cards.
2. The probability of drawing 2 cards that are both aces.
3. The probability of drawing 4 cards all from the same suite.

A group of 10 students made up of 6 females and 4 males form a committee of 4.
What is the probability the committee is all male?
What is the probability that the committee is all female?
What is the probability the committee is made up of 2 females and 2 males?

• Show Video Lesson

How To Find The Probability Of Multiple Independent Events?

This video explains the counting principle and how to determine the number of ways multiple independent events can occur.

Examples:

1. How many ways can students answer a 3-question true of false quiz?
2. How many passwords using 6 digits where the first digit must be letters and the last four digits must be numbers?
3. A restaurant offers a dinner special in which you get to pick 1 item from 4 different categories. How many different meals are possible?
4. A door lock on a classroom requires entry of 4 digits. All digits must be numbers, but the digits can not be repeated. How many unique codes are possible?

• Show Video Lesson

How To Find The Probability Of A Union Of Two Events?

This video shows how to determine the probability of a union of two events.

Examples:

1. If you roll 2 dice at the same time, what is the probability the sum is 6 or a pair of odd numbers?
2. What is the probability of selecting 1 card that is red or a face card?

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.