Parallel Vectors
Related Pages
Vectors
Equal Vectors
Vector Multiplication
Vector Geometry
In these lessons, we will learn how to determine if the given vectors are parallel.
What Are Parallel Vectors?
A vector is a quantity that has both magnitude and direction.
Vectors are parallel if they have the same direction or opposite direction.
Two non-zero vectors, u and v, are parallel if and only if one is a scalar multiple of the other.
Mathematically, vectors u and v are parallel if:
u = kv
where k is a scalar (non-zero real number).
If k > 0, the vectors point in the same direction.
If k < 0, the vectors point in opposite directions (sometimes called anti-parallel).
Both components of one vector must be in the same ratio to the corresponding components of the parallel vector.
Example:
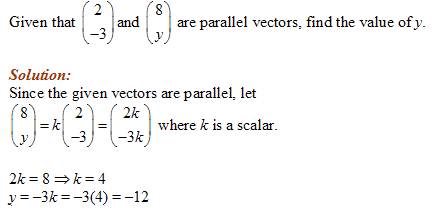
How To Define Parallel Vectors?
Two vectors are parallel if they are scalar multiples of one another.
If u and v are two non-zero vectors and u = cv, then u and v are parallel.
The following diagram shows several vectors that are parallel.
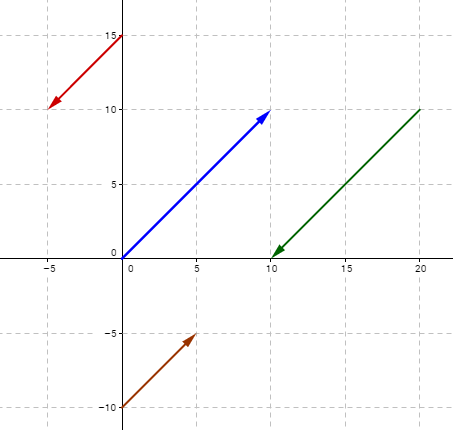
How To Determine If The Given 3-Dimensional Vectors Are Parallel?
Example: Determine which vectors are parallel to v = <-3, -2, 5>
What Are The Conditions For Two Lines To Be Parallel Given Their Vector Equations?
Lines are parallel if the direction vectors are in the same ratio.
Example: If the lines l1: \(r = \left( {\begin{array}{*{20}{c}}1\\{ - 5}\\7\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}{a - 1}\\{ - a - 1}\\b\end{array}} \right)\) and l2: \(r = \left( {\begin{array}{*{20}{c}}9\\3\\{ - 8}\end{array}} \right) + \mu \left( {\begin{array}{*{20}{c}}{2a}\\{3 - 5a}\\{15}\end{array}} \right)\).
Find the values of a and b.
What Is A Vector Is, How To Add And How To Prove Vectors Are Parallel And Collinear?
Examples:
- A, B, C are midpoints of their respective lines. Find the vector OB.
- N = midpoint of OB, M = midpoint of OA. Show that MN is parallel to AB.
- Given the vectors, prove that the three given points are collinear.
How To Answer A Question That Involves Vectors - Lines, Parallel, Perpendicular & Intersection?
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
Penguin Solitaire:
Move all cards to the foundations to build four full sequences. There are two versions here: Penguin (Tuxedo) and Penguin (Original).
Sawayama Solitaire:
This is similar to the common Klondike Solitaire except for a few changes to make it more strategic.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.