Parallel Lines and Perpendicular Lines
In these lessons, we will learn
- how to determine if two lines are parallel when given their slopes.
- how to determine if two lines are perpendicular when given their slopes.
- how to find the equation of a line given a point on the line and a line that is parallel to it.
- how to find the equation of a line given a point on the line and a line that is perpendicular to it.
- how to find parallel lines using Standard Form
- how to find perpendicular lines using Standard Form
Slopes Of Parallel Lines
In Coordinate Geometry, two lines are parallel if their slopes (m) are equal.
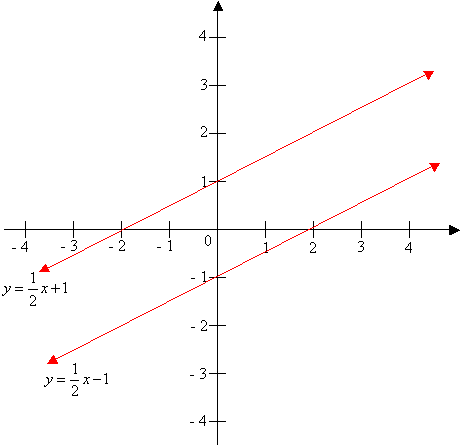
For example: The line
is parallel to the line.
Their slopes are both the same.
In the Coordinate Plane, two lines are perpendicular if the product of their slopes (m) is –1. The slopes are negative reciprocals of each other.
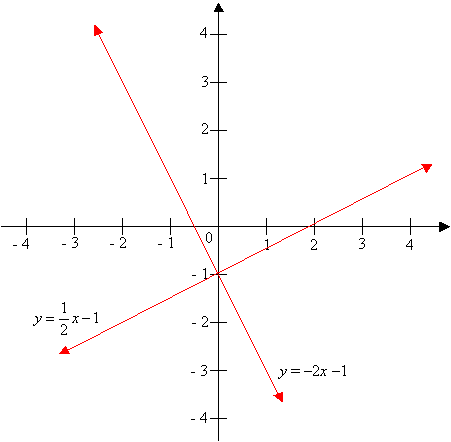
For example: The line
is perpendicular to the line y =
–2x
– 1. The product of the two slopes is
Equation of a line given a point on the line and a line that is parallel to it
The following video shows how write the equation of a line given a point on the line and a line that is parallel to it.Examples:
1) Write the equation of the line parallel to y = 3x - 5 through (1,3)
2) Write the equation of the line parallel to 2x + 3y = 5 through (6,1)
Parallel and Perpendicular lines
This video involves equations of lines that are parallel or perpendicular to a given line, using slope-intercept (y = mx + b) form.
How to find the equation of a line given a point on the line and a line that is parallel to it?
How to find the equation of a line given a point on the line and a line that is perpendicular to it?
Examples:
1. Find the equation of a line that is parallel to x + 7y = 4 and passes through the point (7,9)
2. Find the equation of a line that is perpendicular to y = -9x + 5 and passes through the point (3,9)
3. Find the slope-intercept form of the equation of a line that is parallel to the graphed line and that passes through the point plotted on the graph.
Equation of a line given a point on the line and a line that is perpendicular to it
The following video gives an example of how to find the equation of a line given a point on the line and a line that is perpendicular to it.
Example:
Find the equation of a line perpendicular to the line 3x + 5y = 15 through the point (6, -1)
Find Parallel Lines using Standard Form
Another method to find the equation of a parallel line would be to use the Standard Form of the equation. The following video shows how to find parallel lines using Standard Form.Example:
Find the equation of a line parallel to 8x - 9y = 3 and passing through (2,3)
Find Perpendicular Lines using Standard Form
Another method to find the equation of a perpendicular line would be to use the Standard Form of the equation. The following video shows how to find perpendicular lines using Standard Form.Example:
Find the equation of a line perpendicular to 8x - 9y = 3 and passing through (2,3)
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.