Forms Of Linear Equation
In these lessons, we will learn the various forms of linear equations and how to convert between the different forms.
Related Pages
Linear Equations In Two Variables
Graphing Linear Equations
Coordinate Geometry
Linear Equations or Equations of Straight Lines can be written in different forms.
We shall look at:
- the slope-intercept form for the equation of a line.
- the point-slope form for the equation of a line.
- the general form for the equation of a line.
- the standard form for the equation of a line.
- how to convert between the different forms of linear equations.
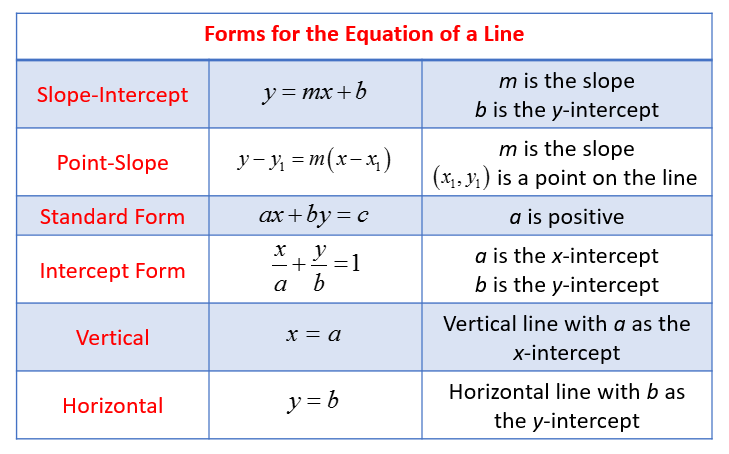
The following table gives the Forms of Linear Equations. Scroll down the page for examples
and solutions.
Slope–Intercept Form
y = mx + b
where m is the slope of the line and b is the y-intercept.
The y-intercept is the y-coordinate of the location where line crosses the y axis. This is the point when x = 0 and y = b.
Vertical lines, having undefined slope, cannot be represented by this form.
The slope-intercept form is useful when we are given the slope and y-intercept of a line and we need to write an equation for the line.
It is also useful because we can read the slope and y-intercept from the equation. Often, when we are given equations in other forms, we can rewrite it in slope-intercept form to get the slope and y-intercept.
The slope-intercept form is also useful when we need to draw the line on a graph.
More examples, videos and explanations about the slope-intercept form and how it can be used.
Point–Slope Form
y − y1 = m(x − x1)
where m is the slope of the line and (x1, y1) is any point on the line.
The point-slope form shows that the difference in the y-coordinate between two points on a line is proportional to the difference in the x coordinate. The proportionality constant is the slope of the line, m.
The point-slope form is useful when we are given a point on a line and the slope and we need to get the equation of the line.
How to find the equation of a line using point-slope form when given two points?
Example:
Find the equation of the line that goes through (-3,5),(2,8)
General Form
Ax + By + C = 0
where A or B can be zero, but not both at the same time.
The equation is usually written so that A ≥ 0. The graph of the equation is a straight line, and every straight line can be represented by an equation in the above form.
If B is not zero, then the slope of the line is −A/B and the y-intercept is −C/B.
If B is zero, then the line Ax + C = 0 is a vertical line with a x-intercept of −C/A.
If A is zero, then the line By + C = 0 is a horizontal line with a y-intercept of −C/B.
The General Form is useful when we want to write equations for vertical lines which is not possible in slope-intercept form or point-slope form. For example, 2x + 5 = 0.
Standard Form
Ax + By = C
where A or B can be zero, but not both at the same time. A, B and C are integers and A ≥ 0. A,
B and C have no common factors other than 1.
When is Standard Form useful?
- When we want to solve systems of linear equations.
- When we want to write equations for vertical lines which is not possible in slope-intercept form or point-slope form. For example, 2x = 5.
- Simplifies finding parallel and perpendicular lines.
How to find parallel lines using Standard Form?
Example:
Find the equation of the line parallel to 8x - 9y = 3 and passing through (2,3)
How to find perpendicular lines using Standard Form?
Example:
- Find the equation of the line perpendicular to 8x - 9y = 3 and passing through (-5,7).
- Find the equation of the line parallel to y = 5 and passing through (-71,89).
- Find the equation of the line perpendicular to y = 5 and passing through (-6,-4).
How to determine the equation of a line in standard form given two points?
This video lesson shows how to determine the equation using slope-intercept form and then how to write the equation in standard form.
Example:
Determine the equation of the line passing through (-1,1) and (1,7). Write the line in standard form.
Convert Between The Different Forms Of Equation
We will look at how to convert between the different forms of equation.
How to convert from Standard Form to Slope Intercept Form?
Example:
Convert the following to slope-intercept form 2x - 3y + 6 = 0
How to convert the point-slope form of the equation of a line to slope-intercept form?
How to convert between point-slope form, slope-intercept form and standard form?
Example:
A line passes through the points (-3,6) and (6,0). Find the equation of this line in:
a) Point-slope form
b) Slope-intercept form
c) Standard form
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.