Mean From Frequency Table With Intervals
Related Pages
Mean From The Frequency Table With Discrete Data
Central Tendency
More Statistics Lessons
In these lessons, we will learn how to find the mean, mode and median from a frequency table for both discrete and grouped data.
How to find the Mean of Grouped Data?
When you have a frequency table with intervals (also known as a grouped frequency table), you don’t have the exact individual data values. Therefore, you cannot calculate the true mean. Instead, you calculate an estimated mean.
The method involves using the midpoint of each interval as a representative value for all the data points within that interval.
The formula to find the mean of grouped data from a frequency table is given below. Scroll down the page for more examples and solutions.
Statistics Worksheets
Practice your skills with the following worksheets:
Printable & Online Statistics Worksheets
How To Find The Mean From A Frequency Distribution Table?
The following example shows how to determine the mean from a frequency table with intervals or grouped frequency table.
Example:
The following table shows the frequency distribution of the diameters of 40 bottles.
(Lengths have been measured to the nearest millimeter) Find the mean of the data.
| Diameter (mm) | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 60 |
|---|---|---|---|---|---|
| Frequency | 6 | 12 | 15 | 10 | 7 |
Solution:
Step 1: Find the midpoint
of each interval.
Midpoint of interval = 
(Lower class limit + Upper class limit)
= 
(39 + 35) = 37
| Diameter (mm) | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 60 |
|---|---|---|---|---|---|
| Frequency (f) | 6 | 12 | 15 | 10 | 7 |
| Mid-point (x) | 37 | 42 | 47 | 52 | 57 |
Step 2: Multiply the frequency of each interval by its mid-point.
| Diameter (mm) | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 60 |
|---|---|---|---|---|---|
| Frequency (f) | 6 | 12 | 15 | 10 | 7 |
| Mid-point (x) | 37 | 42 | 47 | 52 | 57 |
| f × x | 222 | 504 | 705 | 520 | 399 |
Step 3: Get the sum of all the frequencies (f) and the sum of all the fx. Divide ‘sum of fx’ by ‘sum of f ’ to get the mean.
| Total | ||||||
|---|---|---|---|---|---|---|
| Diameter (mm) | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 60 | |
| Frequency (f) | 6 | 12 | 15 | 10 | 7 | 50 |
| Mid-point (x) | 37 | 42 | 47 | 52 | 57 | |
| f × x | 222 | 504 | 705 | 520 | 399 | 2350 |
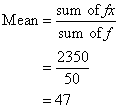
Why is it an “Estimate”?
It’s an estimate because we assume that all data points within an interval are concentrated at its midpoint. This assumption allows us to perform the calculation, but it means the result is an approximation, not the exact mean. The accuracy of the estimate generally improves with narrower class intervals.
How To Find The Mean, Mode And Median From A Frequency Table For Both Discrete And Grouped Data?
Mean: multiply midpoints by frequencies and add the sub-totals. Divide by the total of the frequencies.
Mode: find the largest frequency - the corresponding value is the modal value or modal class.
Median: calculate a running total of the frequencies - the first interval that is above half the total contains the median.
How To Find The Mean From A Frequency Table For Discrete Data And Continuous (Grouped) Data?
How To Get Averages From Grouped Frequency Tables, Including The Range, Mean, Median And Mode?
How To Work Out The Mean From A Grouped Frequency Table?
First work out the midpoints of each group. Then multiply the midpoints by the frequency. Divide the total of this column by the total frequency.
How to use a TI-84 calculator to calculate the Mean and Standard Deviation of a Frequency Distribution?
Find the mean and the standard deviation of the population data summarized by the following frequency distribution.
How to use a TI-84 calculator to calculate the Mean and Standard Deviation of a Grouped Frequency Distribution?
Find the mean and the standard deviation of the sample data summarized by the following frequency distribution.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.