Math Problem Solving Strategies
Related Pages
Solving Word Problems Using Block Models
Heuristic Approach to Problem-Solving
Algebra Lessons
In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.
Problem Solving Strategies
There are numerous math problem-solving strategies that can help you tackle a wide range of mathematical challenges. These strategies provide a structured approach to understanding and solving problems. Here are some of the most common and effective types of math problem-solving strategies:
- Verbal Model & Algebraic Model
A verbal model is a step-by-step description in words that translates a word problem into a mathematical equation or relationship. It helps organize information logically before writing equations. It’s a way to bridge the gap between the narrative of the word problem and the mathematical operations needed to find the solution.
How to create a Verbal Model?
Analyze and read the problem carefully.
- What do you know?
- What do you need to know?
- Draw a diagram/picture
Solution Strategy
- Label Variables
Use variables for things that you need to find. - Verbal Model or Logical Reasoning
Explain your way of finding the solution. - Algebraic Model
Translate Verbal Model to Algebraic Model. - Solve and Check
Algebra Word Problems & Worksheets
Examples and solutions for the different types of Algebra math word problems:
Algebra Math Word Problems
Practice your problem solving skills with the following word problems worksheets:
Algebra Math Word Problems Worksheets
Steps for Solving Word Problems
Step 1: Identify (What is being asked?)
Step 2: Strategize
Step 3: Write the equation(s)
Step 4: Answer the question
Step 5: Check
- Block Model/Bar Model/Tape Diagrams
Solving word problems using block models (also known as bar models or tape diagrams) is a visual strategy that helps break down the information in a problem and make the relationships between quantities clearer. It’s particularly effective for problems involving addition, subtraction, multiplication, division, and fractions. It is used in Singapore Math to help students visualize and solve word problems without using Algebra.
Solving Word Problems using Block Models
Solving Word Problems using Singapore Math
- Guess and Check Model
Using the guess and check problem solving strategy to help solve math word problems.
Example:
Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills.
If she gave the clerk 10 bills in all, how many of each bill did she use?
- Find a Pattern Model
Make A Table And Look For A Pattern - Identify - What is the question?
- Plan - What strategy will I use to solve the problem?
- Solve - Carry out your plan.
- Verify - Does my answer make sense?
Example:
Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2
more than the previous day. How much money did Marcus made in all after 5 days?
Find A Pattern Model (Intermediate)
In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.
You can also check out the following pages for basic and advanced examples using the Find a Pattern Model.
Find a Pattern Model (Basic)
Find a Pattern Model (Intermediate)
Example:
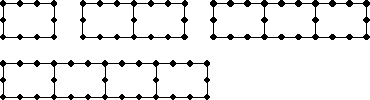
The figure shows a series of rectangles where each rectangle is bounded by 10 dots.
a) How many dots are required for 7 rectangles?
b) If the figure has 73 dots, how many rectangles would there be?
Example:
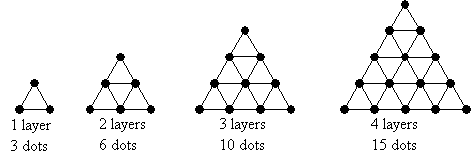
Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7
layers of triangles.
Example:
The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the
following numbers belong?
a) 25
b) 46
c) 269
| I | 1 | 7 | 13 | 19 | 25 |
| II | 2 | 8 | 14 | 20 | 26 |
| III | 3 | 9 | 15 | 21 | 27 |
| IV | 4 | 10 | 16 | 22 | |
| V | 5 | 11 | 17 | 23 | |
| VI | 6 | 12 | 18 | 24 |
Example:
The following figures were formed using matchsticks.
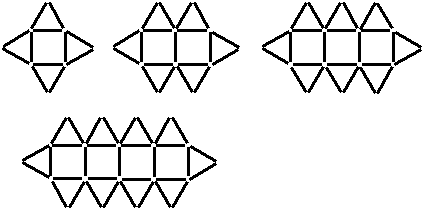
a) Based on the above series of figures, complete the table below.
| Number of squares | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number of triangles | 4 | 6 | 8 | 10 | ||||
| Number of matchsticks | 12 | 19 | 26 | 33 |
b) How many triangles are there if the figure in the series has 9 squares?
c) How many matchsticks would be used in the figure in the series with 11 squares?
Example:
Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many
handshakes were there?
The following video shows more examples of using problem solving strategies and models.
Question 1: Approximate your average speed given some information
Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row.
Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?
The following are some other examples of problem solving strategies.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.