Problem-Solving Strategies: Finding Patterns

The following are some examples of problem solving strategies.

Explore it/Act it/Try it (EAT) method (Basic)
Explore it/Act it/Try it (EAT) method (Intermediate)
Explore it/Act it/Try it (EAT) method (Advanced)
Finding a Pattern (Basic)
Finding a Pattern (Intermediate)
Finding a Pattern (Advanced)

Find A Pattern (Advanced)

Here we will look at some advanced examples of “Find a Pattern” method of problem solving strategy.

Example:
Each hexagon below is surrounded by 12 dots.
a) Find the number of dots for a pattern with 6 hexagons in the first column.
b) Find the pattern of hexagons with 229 dots.

Solution:

1st column	Pattern	Total dots
1	12	12
2	12 + 16	28
3	12 + 16 + 21	49
4	12 + 16 + 21 + 26	75
5	12 + 16 + 21 + 26 + 31	106
6	12 + 16 + 21 + 26 + 31 + 36	142
7	12 + 16 + 21 + 26 + 31 + 36 + 41	183
8	12 + 16 + 21 + 26 + 31 + 36 + 41 + 46	229

a) The number of dots for a pattern with 6 hexagons in the first column is 142.

b) If there are 229 dots then the pattern has 8 hexagons in the first column.

Example:
Each member of a club shook hands with every other member who came for a meeting. There were a total of 45 handshakes. How many members were present at the meeting?

	A	B	C	D	E	F	G	H	I	J
A
B	●
C	●	●
D	●	●	●
E	●	●	●	●
F	●	●	●	●	●
G	●	●	●	●	●	●
H	●	●	●	●	●	●	●
I	●	●	●	●	●	●	●	●
J	●	●	●	●	●	●	●	●	●
HS	9	8	7	6	5	4	3	2	1

Solution:
Total = 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 handshakes

There were 10 members

Example:
In the figure, a pinball is released at A.

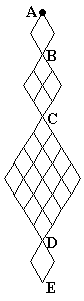
How many paths are there for it to drop from A to E?

Solution:
from A to B: 2
B to C: 6
A to C: 2 × 6 = 12
C to D: 70
A to D: 12 × 70 = 840
D to E: 2
A to E: 2 × 840 = 1680

There are 1680 paths from A to E

Example:
A group of businessmen were at a networking meeting. Each businessman exchanged his business card with every other businessman who was present.

a) If there were 16 businessmen, how many business cards were exchanged?

b) If there was a total of 380 business cards exchanged, how many businessmen were at the meeting?

Solution:
a) 15 + 14 + 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 120 exchanges

120 × 2 = 240 business cards

If there were 16 businessmen, 240 business cards were exchanged.

b) 380 ÷ 2 = 190

190 = (19 × 20) ÷ 2 = 19 + 18 + 17 + … + 3 + 2 + 1

If there was a total of 380 business cards exchanged, there were 20 businessmen at the meeting.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.