Algebra: Lever Word Problems

Lever Word Problems

Lever Problems are word problems that use the lever principle. A good example of a lever is the seesaw.

A lever can be set up with unequal weights placed at different distances from the balancing point (also called the fulcrum).

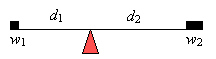
In order for the above lever to be balanced, the following equation must be satisfied.

w₁ × d₁ = w₂ × d₂

Sketching a diagram of the situation is usually helpful in solving lever problems.

• Algebra Word Problem Worksheets

  Printable
  Words to Equations
  Algebra Word Problems
  Angle Word Problems (6th Grade)
  Angle Word Problems (7th Grade)
  

  Inequality Word Problems
  

  Word Problems (Multiplication & Division)
  2-Step Word Problems (Multiply/Divide/Add/Subtract)
  Multi-step Word Problems (using +, -, ×)
  

Lever Problems: Two Objects

Example 1:
John weighs 90 lbs and Jane weighs 60 lbs. They are both seating on a seesaw. If John is seated 10 feet away from Jane, how far should each be from the fulcrum of the seesaw?

Solution:
Step 1: Assign variables:

Let x = distance of John from the fulcrum
Let 10 - x = distance of Jane from the fulcrum

Step 2: Sketch the diagram

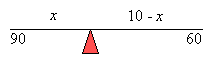
Step 3: Obtain equation from the diagram

90(x) = 60(10 – x)

Use the Distributive Property
90x = 600 – 60x

Isolate variable x
90x + 60x = 600
150x = 600
x = 4

Answer: John should be 4 feet and Jane should be 6 feet from the fulcrum.

Example 2:
John wants to move a 400 lb. rock with a 5 ft. 9 in. crowbar. He puts the fulcrum 9 inches from the rock. How much force must he use to move the rock?

Solution:
Step 1: Assign variables :

Let x = force used
Change 5 ft. to 5 × 12 = 60 inches

Step 2: Sketch the diagram

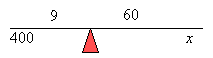
Step 3: Obtain equation from the diagram

9 × 400 = 60 × x

Isolate variable x
60x = 3600
x = 60

Answer: He must use a force of 60 lbs.

Algebra Word Problem: Lever Problems

Seesaw Problem

Example:
Danny is 60lbs, Maria is 40lbs, both are balanced on seesaw that is 10ft. If the fulcrum is x ft away from Danny, what is x?

• Show Video Lesson

Example:
John weighs 80 pounds and sits 4 feet from the fulcrum of a seesaw. If Sally weighs 100 pounds and sits on the other side, how far from the fulcrum must she sit to have the seesaw balance?

Lever Problems: More than Two Objects

Example:
John, Peter and Jane weigh 80, 60 and 50 lbs respectively. John sits 3 ft., Peter sits 5 ft. and Jane sits 6 ft. from the fulcrum on the same side. How far must their 200 lb. father sits from the fulcrum in order to balance them?

Solution:
Step 1: Assign variables :

Let x = distance of father from fulcrum

Step 2: Sketch the diagram

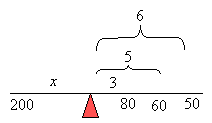
Step 3: Obtain equation from the diagram

200 × x = 3 × 80 + 5 × 60 + 6 × 50

Isolate variable x
200x = 240 + 300 + 300
200x = 840
x = 4.2

Answer: Their father must sit 4.2 ft. from the fulcrum.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.