Identity Property
Related Pages
Identity Property Of Addition, Multiplication
More Lessons On Numbers
Math Worksheets
The basic Number Properties (or laws) that apply to arithmetic operations are Commutative Property, Associative Property, Identity Property and Distributive Property.
The following table gives the commutative property, associative property and identity property for addition and subtraction. Scroll down the page for more examples and solutions of the number properties.
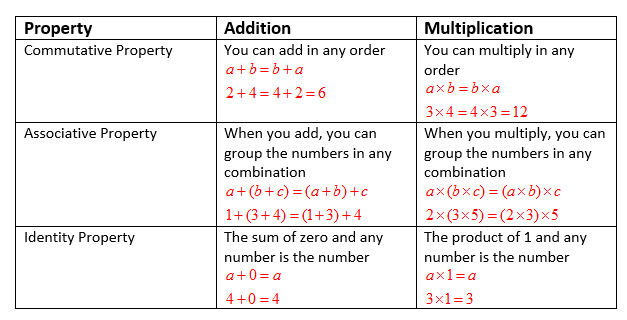
Commutative Property
The Commutative Property says that you can move numbers around in an equation without changing the result.
For Addition: The order of the numbers doesn’t matter.
5+3=3+5
For Multiplication: The order of the numbers doesn’t matter.
4×6=6×4
This property doesn’t work for subtraction or division.
Associative Property
The Associative Property says that you can group numbers differently in an addition or multiplication problem without changing the answer. This is useful when you have more than two numbers.
For Addition: You can group the numbers in any way.
(2+3)+4=2+(3+4)
For Multiplication: You can group the numbers in any way.
(2×3)×4=2×(3×4)
This property doesn’t work for subtraction or division.
Identity Property
The Identity Property involves a special number that, when used in an operation, leaves the original number unchanged.
For Addition: The identity element is zero (0).
5+0=5
For Multiplication: The identity element is one (1).
7×1=7
Distributive Property
This property connects multiplication with addition or subtraction. It says that you can “distribute” the number you are multiplying to each part inside the parentheses.
For Multiplication over Addition:
3×(4+2)=(3×4)+(3×2)
3×6=12+6
18=18
This property is what allows you to break down complicated problems into simpler parts.
Zero Property Of Multiplication
The product of any number and 0 is 0.
For example: 874 × 0 = 0
Videos
Identity Property Of Addition And Multiplication
Identity Property of addition states that any number plus zero is the original number.
Identity property of multiplication states any number times one is the original number.
Identity Property
This video defines the Identity Property.
The Identity Property is made up of two parts: Additive Identity and Multiplicative Identity.
The Additive Identity is
Add zero (0) to a number, the sum is that number.
The Multiplicative Identity is
Multiply a number by 1, the Product is that number.
Divide a number by itself, the Quotient is 1.
Commutative And Zero Properties Of Multiplication
Commutative, Associative And Identity Properties
Example:
-
Tell which property is represented
a) (2 ˙ 6) ˙ 1 = 2 ˙ (6 ˙ 1)
b) 3 + 0 = 3
c) 7 + 9 = 9 + 7 -
Simplify each expression. Justify each step.
a) 17 + 14 + 3
b) 12 ˙ 3 ˙ 5
c) 21 + 16 + 9
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.