Graph Linear & Quadratic Functions

Graph linear and quadratic functions and show intercepts, maxima, and minima.

Common Core: HSF-IF.C.7

• Graph quadratic functions expressed in various forms by hand.
• Use technology to model quadratic functions, when appropriate.
• Graph and find key features of piecewise-defined functions, including step functions and absolute value functions.

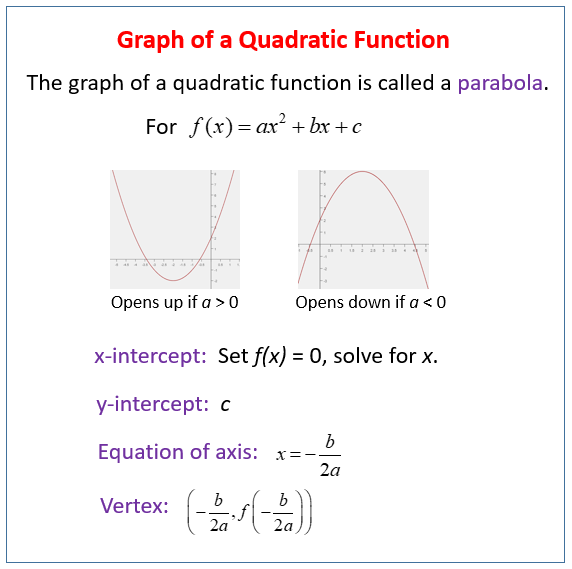
The following figure shows how to graph a quadratic function in general form. Scroll down the page for more examples and solutions on graphing quadratic functions.

Ex: Graph a Linear Function Using a Table of Values
This video provides and example of how to graph a linear function by completing a table of values.

• Show Step-by-step Solutions

Graphing Quadratic Functions in General Form or Standard Form
This video explains how to graph quadratic functions in the form f(x) = ax²+ bx + c.
The graph of a quadratic function is called a parabola.
a) It is always a cup-shaped curve.
b) It opens upward if a > 0 or opens downward if a < 0
c) The vertical line x = -b/2a is the line of symmetry.
d) It has a turning point, or vertex, at the point (-b/2a, f(-b/2a)).

Examples:

1. Graph f(x) = x² - 4x - 5. Find the equation of the axis of symmetry, the vertex, and the x-intercepts.
   
2. Given f(x) = x² + 10x - 7, find the equation of the axis of symmetry, the vertex. Then graph with the help of a graphing calculator.
   

• Show Step-by-step Solutions

Ex1: Graph a Quadratic Function in General Form
This video explains how to determine the x and y intercepts, equation of the axis of symmetry, and the vertex in order to graph a quadratic function. The function is factorable.
Examples:

1. Given f(x) = x² - x - 56, find the following and then graph. x-intercepts, y-intercept, equation of axis, vertex.
   
2. Given f(x) = x² - x - 6, find the following and then graph. x-intercepts, y-intercept, equation of axis, vertex.
   

• Show Step-by-step Solutions

** Ex2: Graph a Quadratic Function in General Form**
This video explains how to determine the x and y intercepts, equation of the axis of symmetry, and the vertex in order to graph a quadratic function. The function is NOT factorable.
Examples:
Given f(x) = -x² + 4x + 2, find the following and then graph. x-intercepts, y-intercept, equation of axis, vertex.

• Show Step-by-step Solutions

Graphing Quadratic Functions Using Symmetric Points
This video provides an alternative method for graphing quadratic functions using symmetric points and the vertex.

1. Factor out the GCF of the two x-terms.
   
2. Select the two x-values that make the factored part equal to zero. Then find the corresponding y-values. Plot these two points.
   
3. Determine the x-value between the two points. This will be the coordinate of the vertex. Find the corresponding y-value. Plot the vertex.
   
4. Graph the function.
   Examples:
   Graph the quadratic function.
   y = -2x² + 6x - 1
   f(x) = 1/2 x² -x - 2
   

• Show Step-by-step Solutions

Graphing Quadratic Functions in Vertex Form
This video explains how to graph quadratic functions in the form f(x) = a(x-h)² + k.
The vertex of the parabola occurs at the point (h,k), and the vertical line passing through the vertex is the axis of the parabola.
Example:

1. Graph and identify the vertex, axis of symmetry, and the intercepts.
   f(x) = (x - 3)² - 4
   
2. Graph and identify the vertex, axis of symmetry, and at least two additional points.
   f(x) = -2(x + 1)² + 8
   

• Show Step-by-step Solutions

** Quadratic Functions - Find Vertex and Intercepts Using the Graphing Calculator**
This video explains how to find the vertex, y-intercept, and x-intercepts of a quadratic function on the TI-84 graphing calculator.
Example:
f(x) = 2x² - 14x + 7
Find the vertex, the y-intercept or vertical intercept, the x-intercepts or horizontal intercepts.

• Show Step-by-step Solutions

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.