Factor Trinomials with Two Variables

Factoring Trinomials with two Variables

Factoring trinomials with two variables, often in the form of ax² + bxy + cy², is very similar to factoring trinomials with a single variable (ax² + bx + c). The key difference is how the second variable (y) is distributed in the factored binomials.

The following diagram shows how to factor trinomials with two variables when the leading coefficient is one. Scroll down the page for more examples and solutions.

 

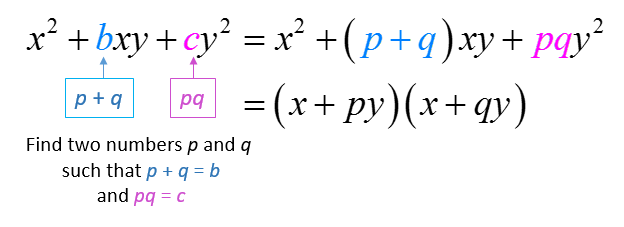
• Factor Trinomial Worksheets

  Printable
  Factoring Trinomials (a = 1)
  Factoring Trinomials (a > 1)
  Factor Perfect Square Trinomials
  

  Factoring Quadratics (a = 1)
  Factoring Quadratics (a > 1)
  Factor Difference of Squares
  Factor Perfect Square Quadratics
  

  Online
  Factor Binomials by Difference of Squares
  Factor Perfect Square Trinomials
  
  Factor Trinomials or Quadratic Equations
  Factor Different Types of Trinomials 1
  Factor Different Types of Trinomials 2
  
  Solve Trinomials using Quadratic Formula
  Find Discriminants of Quadratic Polynomials

Steps to Factor Trinomials with Two Variables by Grouping:
We can use the “ac method” (or grouping method), extended for two variables.
General Form: ax² + bxy + cy²

1. Check for a Greatest Common Factor (GCF):
   Always begin by looking for a GCF among all three terms. If found, factor it out first.
   
2. Find Two Numbers that Multiply to “ac” and Add to “b”:
   Find two numbers (let’s call them p and q) such that:
   p × q = ac
   p + q = b
   
3. Rewrite ax² + bxy + cy² as
   ax² + pxy + qxy + cy²
   
4. Group the first two terms and the last two terms:
   (ax² + pxy) + (qxy + cy²)
   
5. Factor Out the GCF from Each Pair:
   Factor out the greatest common monomial factor from the first group.
   Factor out the greatest common monomial factor from the second group.
   The binomial remaining inside the parentheses after factoring out the GCF must be identical for both pairs. If it’s not, recheck your numbers in the above steps.
   
6. Factor out the common binomial to form the product of two binomials.
   
7. Check Your Answer: Multiply your two binomial factors back together using FOIL or distributive property to ensure you get the original trinomial.

Videos

How to factor Trinomials with two variables?
Sometimes a trinomial may consists of two variables. We can factor the trinomial in a similar way as if it has only one variable. We can use the trial and error method (reverse FOIL method), the grouping method or the AC method.

Example:
Factor the following trinomials:
a) e² − 6ef + 9f²
b) 2x² + 7xy − 15y²

Solution:
a) e² − 6ef + 9f² = (e − 3f)²
b) 2x² + 7xy − 15y² = (2x − 3y)(x + 5y)

Factoring trinomials with two variables
Step 1: Find the Product, Sum and the two numbers that “work”
Product = (First number) × (Last number)
Sum = (Middle Number)
Find two numbers that when multiplied gives the Product and when added gives the Sum.
Step 2: Split the middle term.
Step 3: Group in twos and remove the GCF of each group.
Step 4: Write in factored form.

How to factor trinomials with two variables and a = 1?
Some strategies to factor trinomials that have a = 1

Examples:

1. a² - 9ab + 14b²
2. m² - mn - 30n²

• Show Video Lesson

How to factor trinomial with two variables and a > 1?

Example:
18m² - 9mn - 2n²

• Show Video Lesson

Factor trinomial containing two variables
Example:
v² + 5vf - 24f²

• Show Video Lesson

How to factor trinomial with two variables using gcf then grouping?
Example:
6m⁶n + 11m⁵n² + 3m⁴n³

• Show Video Lesson

How to factor a trinomial with two variables using the AC Method?
Example:
30x³y - 25x²y² - 30xy³

• Show Video Lesson

How to Factor Trinomials with Two Variables using the reverse FOIL or trial and error method?
Examples:

1. 12x² - 5xy - 2y²
2. 6x² - 17xy + 10y²

• Show Video Lesson

Example:

1. 2c² + 13cd + 6d²
2. 5x² - 6xy + 1

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.