Exterior Angles Of A Triangle
Related Pages
Exterior Angle Theorem
Types Of Triangles
Interior Angles of a Triangle
Angles In A Triangle
In these lesson, we will learn
- about exterior angles of triangles
- how to find the unknown exterior angle of a triangle
- how to prove that the sum of exterior angles of a triangle is 360°
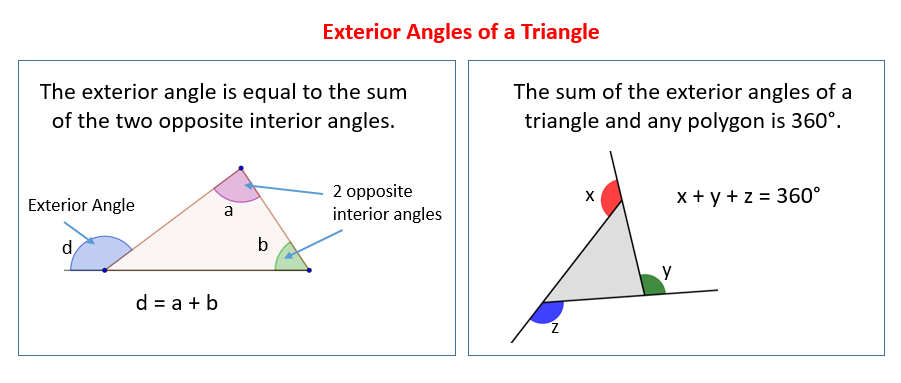
Exterior Angle of a Triangle
An exterior angle of a triangle is formed when one side of the triangle is extended beyond its vertex. It is the angle between the extended side and the adjacent side of the triangle.
The following diagrams give the theorems involving the exterior angles of triangles. Scroll down the page for more examples and solutions.
Geometry Worksheets
Exterior Angle Worksheets
Printable & Online Geometry Worksheets
Properties:
- Exterior Angle Theorem:
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles (also called remote interior angles). - Sum of Exterior Angles:
The sum of the measures of the exterior angles of any triangle (one at each vertex) is always 360 degrees. - Relationship with Interior Angles:
At each vertex, the exterior angle and the interior angle are supplementary (they add up to 180°)
Exterior Angles Of A Triangle
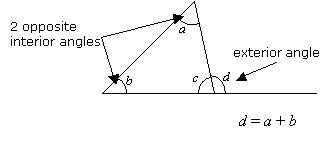
An exterior angle of a triangle is formed by any side of a triangle and the extension of its adjacent side.
The Exterior Angle Theorem states that
An exterior angle of a triangle is equal to the sum of the two
opposite interior angles.
Example:
Find the values of x and y in the following triangle.
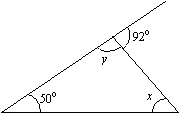
Solution:
x + 50° = 92° (sum of opposite interior angles = exterior angle)
x = 92° – 50° = 42°
y + 92° = 180° (interior angle + adjacent exterior angle = 180°.)
y = 180° – 92° = 88°
What is an exterior angle and how to find the unknown exterior angle of a triangle?
The angles on a straight line add up to 180°.
The interior angles of a triangle add up to 180°
An exterior angle of a triangle is formed when any side is extended outwards.
How to find a missing angle outside of a triangle?
How to define the interior and exterior angles of a triangle and then state several theorems involving the interior and exterior angles of a triangle
The exterior angles of a triangle are the angles that form a linear pair with the interior angles by extending the sides of a triangle.
The sum of the exterior angles of a triangle and any polygon is 360 degrees.
The remote angles are the two angles in a triangle that are not adjacent angles to a specific exterior angle.
The sum of the remote interior angles is equal to the non-adjacent exterior angle.
Sum Of Exterior Angles Of A Triangle
Two column proof of the sum of the exterior angles of a triangle is 360 degrees.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.