Use Exponents to Name Place Value Units

Solutions, examples, and videos to help Grade 5 students learn how to use exponents to name place value units and explain patterns in the placement of the decimal point.

Common Core Standards: 5.NBT.1, 5.NBT.2, 5.MD.1

New York State Common Core Math Grade 5, Module 1, Lesson 3
Worksheets for Grade 5

The following figure gives the place value chart using exponents to represent each place value. Scroll down the page for examples and solutions.

 

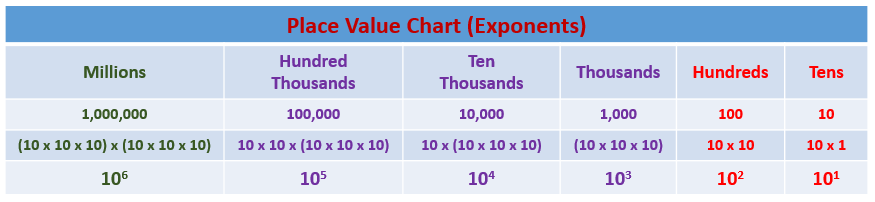
Grade 5 Lesson 3 Concept Development

Problem 1:
Problem 2: Write ten to the fifth power as a product of tens.
Problem 3: 10 × 100
Problem 4: 3 × 10²
Problem 5: 3.4 × 10³
Problem 6: 700 ÷ 10²
Problem 7: 7.1 ÷ 10²

• Show Step-by-step Solutions

Lesson 3 Problem Set

1. Write the following in exponential form (e.g., 100 = 10²).
   a. 10,000 = _____
   b. 1000 = _____
   c. 10 × 10 = _____
   d. 100 × 100 = _____
   e. 1,000,000 = ______
   f. 1000 × 1000 = _____
2. Write the following in standard form (e.g., 5 × 10²= 500).
   a. 9 × 10³ = _____
   b. 39 × 10⁴ = _____
   c. 7200 ÷ 10² = _____
   e. 4.025 × 10³ = _____
   f. 40.25 × 10⁴ = _____
   g. 725 ÷ 10³ = _____

• Show Step-by-step Solutions

This video shows how exponents work in relation to place value. Charts are used to compare exponential form, standard form, and expanded form. Multiplication problems are solved using place value charts.

3. Complete the patterns.
   a. 0.02 0.2 ____ 20 ___ ___

• Show Step-by-step Solutions

Lesson 3 Exit Ticket

1. Write the following in exponential form and as a multiplication sentence using only 10 as a factor (e.g., 100 = 10² = 10 × 10).
   a. 1,000 = ______________ = ______________
   b. 100 × 100 = ______________ = ______________
2. Write the following in standard form (e.g., 4 × 10² = 400).
   a. 3 × 10² = ______________
   c. 800 ÷ 10² = ______________
   b. 2.16 × 10⁴= ______________
   d. 754.2 ÷ 10³ = ______________

Use exponents to name place value units and explain patterns in the placement of the decimal point.

• Show Step-by-step Solutions

Lesson 3 Homework

1. Write the following in exponential form (e.g., 100 = 10²).
   a. 1000 = _____
   b. 10 × 10 = ____
   c. 100,000 = ____
   d. 100 × 10 = ____
   e. 1,000,000 = ____
   f. 10,000 × 10 = ____
2. Write the following in standard form (e.g., 4 × 10² = 400).
   a. 4 × 10³ =
   b. 64 × 10⁴ =
   c. 5300 ÷ 10² =
   d. 5,300,000 ÷ 10³ =
   e. 6.072 × 10³ =
   f. 60.72 × 10⁴ =
   g. 948 ÷ 10³ =
   h. 9.4 ÷ 10² =
3. Complete the patterns.
   a. 0.02 0.2 _____ 20 _____ _____
   b. 3,400,000 34,000 ____ 3.4 _____
   c. _____ 8,570 _____ 85.7 8.57 _____
   d. 444 4440 44,400 _____ _____ _____
   e. ____ 9.5 950 95,000 _____ _____
4. After a lesson on exponents, Tia went home and said to her mom, “I learned that 10⁴ is the same as 40,000.” She has made a mistake in her thinking. Use words, numbers or a place value chart to help Tia correct her mistake.
5. Solve 247 ÷ 10² and 247 × 10². a. What is different about the two answers? Use words, numbers or pictures to explain how the decimal point shifts.
   b. Based on the answers from the pair of expressions above, solve 247 ÷ 10³ and 247 × 10³.

• Show Step-by-step Solutions

• Show Step-by-step Solutions

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.